Take a look at the diagram below.
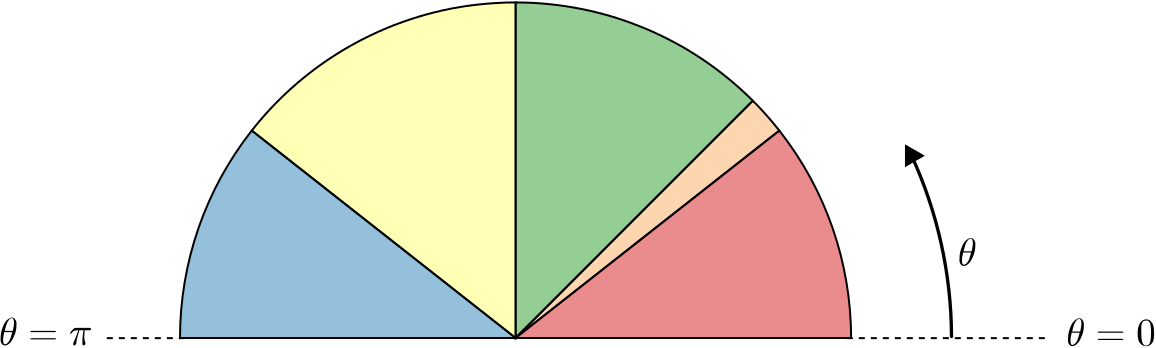
We’ve used inequalities involving \(\sin \theta\), \(\cos \theta\) and \(\tan \theta\) to divide the semicircle into sectors.
Each sector in the diagram is defined by a different inequality.
For example, one sector is defined by the angles \(\theta\) between \(0\) and \(\pi\) for which \(\cos \theta < \sin \theta < \tan \theta.\)
Another sector is defined by \(\cos \theta< \tan \theta < \sin \theta.\)

