In the tables below, \(0\leq \theta \leq 2\pi\) and any missing functions are from the following list. \[\sin \theta \quad \cos \theta \quad \tan \theta \quad \sec \theta \quad \cosec \theta \quad \cot \theta\]
Some of the row and column headings are missing. Without using a calculator, try to work out what they could be and complete the table. A function does not appear twice in the same table.
| \(\theta= \ldots\) | \(\theta= \ldots\) | \(\theta= \ldots\) | |
|---|---|---|---|
| \(-1\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{1}{2}\) | |
| \(\tan \theta\) | undefined | \(\sqrt{3}\) | |
| \(\sec \theta\) | \(-\dfrac{2}{\sqrt{3}}\) |
We have lots of tools that could be used to tackle this problem without relying on a calculator. For example, we could
use sketch graphs of the functions
use special values of the functions, such as \(\cos \tfrac{\pi}{3} = \tfrac{1}{2}\) and \(\tan \tfrac{\pi}{4}=1\)
use triangles or trigonometric identities to work out values of some functions from the values of others
use the unit circle diagram and symmetry to work out values of functions for angles bigger than \(\tfrac{\pi}{2}.\)
We will use a mixture of these tools as we describe two approaches to completing the first table.
Approach 1
If \(\tan \theta\) is undefined then \(\cos \theta=0.\) Therefore \(\sec \theta\) is also undefined and the only possibilities for \(\theta\) in the first column are \(\tfrac{\pi}{2}\) and \(\tfrac{3\pi}{2}.\)
As \(\cot \tfrac{\pi}{2}=\cot \tfrac{3\pi}{2}=0\) the missing function must be \(\sin \theta\) or \(\cosec \theta\), both of which are \(-1\) only when \(\theta = \tfrac{3\pi}{2}\), so in the first column \(\theta = \tfrac{3\pi}{2}.\)
We need more information to decide whether the missing function is \(\sin \theta\) or \(\cosec \theta.\)
From the top row of the table we see that the value of the missing function can be \(\tfrac{1}{2}\), so it must be \(\sin \theta.\)
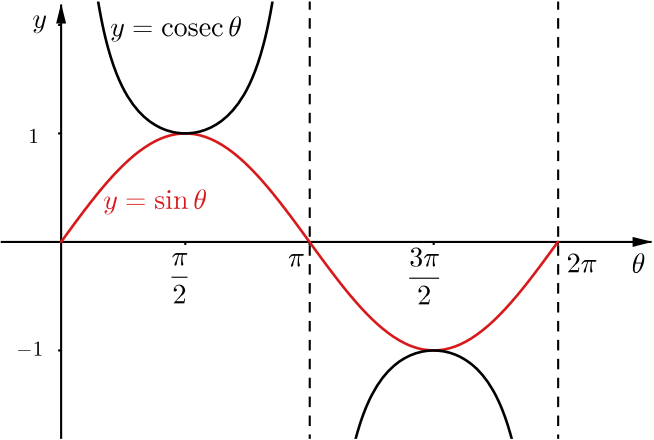
Now, \(\tan \theta = \dfrac{\sin \theta}{\cos \theta} = \sin \theta \sec \theta.\) This means that we can complete the remaining cells in the table without knowing the values of \(\theta.\)
To find the values of \(\theta\), we can recognise certain special values in the table, such as \(\tfrac{\sqrt{3}}{2} =\sin \tfrac{\pi}{3}\) and \(\tfrac{1}{2}=\sin \tfrac{\pi}{6}\), but we need to decide whether this means that the values of \(\theta\) are \(\tfrac{\pi}{3}\) and \(\tfrac{\pi}{6}\) or angles related to them, such as \(\tfrac{\pi}{3}+\pi.\)
From the graphs of these functions, we can check where the functions are positive and negative to decide on the values of \(\theta.\)
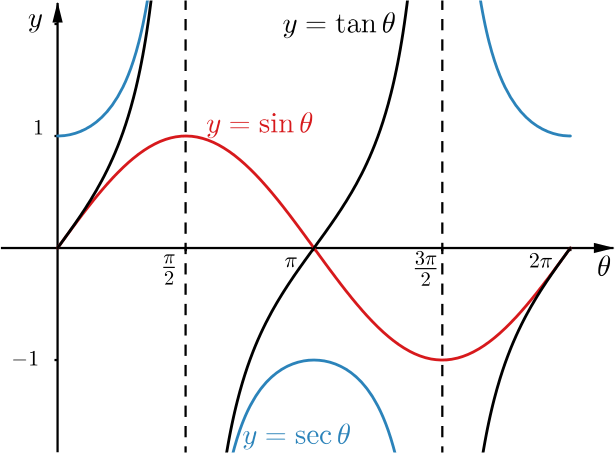
Approach 2
An alternative starting point would be to note that in the third column, \(\cos \theta = -\tfrac{\sqrt{3}}{2}\), so \(\theta\) must be \(\tfrac{5\pi}{6}\) or \(\tfrac{7\pi}{6}.\) The only function which has value \(\tfrac{1}{2}\) at either of these values of \(\theta\) is \(\sin \theta\), and it only takes this value when \(\theta = \tfrac{5\pi}{6}.\) The table can now be completed using a similar argument to the one given above.
How might the answers change if \(\theta\) could be any value?
What if you could use functions like \(- \sin \theta\) to complete the table?
We were limited to \(0\leq \theta \leq 2\pi.\) Otherwise \(\theta\) could take any value of the form \(\dfrac{\pi}{3}+2n\pi\) and \(\dfrac{5\pi}{6}+2n\pi\) where \(n\) is an integer. If we were allowed to use functions such as \(- \sin \theta\) then the problem does not have a unique solution.
This time we have given some more information about \(\theta.\) Try to identify the missing functions and complete the table. Remember not to use a calculator!
| \(\theta\) is reflex | \(\theta= \ldots\) | \(\theta\) is obtuse | |
|---|---|---|---|
| \(0\) | \(-\dfrac{3}{5}\) | ||
| \(\cosec \theta\) | \(1\) | \(\dfrac{5}{4}\) | |
| \(\dfrac{5}{12}\) | \(0\) |
Let’s start with the second column because we know where certain functions are \(1\) or \(0.\) Again, \(\theta\) is limited to \(0\leq \theta \leq 2\pi\), so \(\cosec \theta = 1\) is only true when \(\theta\) is \(\tfrac{\pi}{2}.\) We can now think about which functions are \(0\) when \(\theta = \tfrac{\pi}{2}.\) Since \(\tan \tfrac{\pi}{2}\) and \(\sec \tfrac{\pi}{2}\) are undefined, the only possibilities for the missing functions are \(\cos \theta\) and \(\cot \theta.\)
As both \(\cos \theta\) and \(\cot \theta\) could be \(\tfrac{5}{12}\) and \(-\tfrac{3}{5}\), we need more information to decide which function goes in the top row and which goes in the bottom row (remember that a function cannot appear twice in the table). Both \(\cos \theta\) and \(\cot \theta\) are negative when \(\theta\) is obtuse and both can be negative or positive when \(\theta\) is reflex, so the signs don’t help us here.
Instead, we could use the value of \(\cosec \theta\) in the third column. One of the Pythagorean identities for trigonometric functions tells us that \(\cosec^2 \theta \equiv 1 + \cot^2 \theta.\)
If \(\cot \theta\) were the correct function for the top row, then substituting \(-\tfrac{3}{5}\) for \(\cot \theta\) and \(\tfrac{5}{4}\) for \(\cosec \theta\) should satisfy this identity. If these values don’t satisfy the identity, then we will know that \(\cot \theta\) can’t be the function in the top row.
Once we know where \(\cot \theta\) and \(\cosec \theta\) go, we can use trigonometric identities to complete the table, taking into account the signs of these functions for reflex angles.
- How can you also state the values of \(\theta\) in the \(1\)st and \(3\)rd columns?
We can express \(\theta\) in the third column as \(\arccos \left(-\tfrac{3}{5}\right)\), but in the first column \(\theta\) cannot be written \(\arccos \left(-\tfrac{5}{13}\right)\) because of the principal value range of \(\arccos.\) How is this value of \(\theta\) related to \(\arccos \left(-\tfrac{5}{13}\right)\)?
We could also use \(\mathrm{arccot}\) or \(\mathrm{arccosec}\) and it could be interesting to think about what their principal value ranges must be.

