An aeroplane can fly at \(\quantity{300}{km/h}\) in still air. If a steady \(\quantity{60}{km/h}\) wind is blowing from the direction \(030^\circ\), determine
- the direction in which the aeroplane must head in order that it actually flies due North,
We can draw a diagram of the velocity vectors for the wind and the aeroplane.
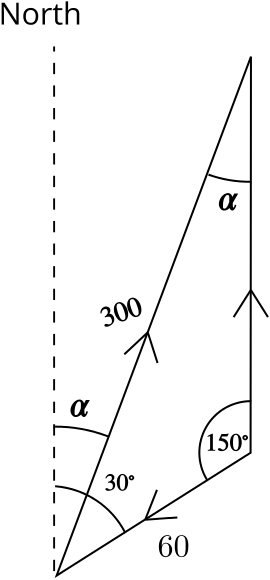
We can now use the sine rule to find the angle \(\alpha\). We have
\[\begin{align*} \frac{\sin \alpha}{60} &= \frac{\sin 150^\circ}{300}\\ \alpha &= \sin^{-1} \frac{\sin 150^\circ}{5} = 5.739...^\circ. \end{align*}\]The aeroplane needs to take a bearing of \(006^\circ\) (to the nearest degree) to counteract the wind and fly due north.
- the aeroplane’s resultant velocity.
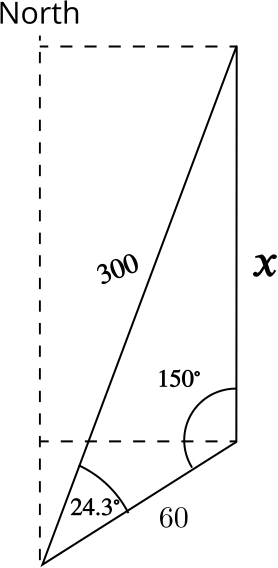
Using the sine rule
The angle between the velocity vectors of wind and aeroplane is \(30^\circ - \alpha = 24.261...^\circ\). Hence we find
\[\begin{align*} \frac{\sin 150^\circ}{300} &= \frac{\sin 24.261^\circ}{x}\\ x&=300 \frac{\sin 24.261^\circ}{\sin 150^\circ}. \end{align*}\]This gives a final velocity of the aeroplane of \(v = 246.54...\approx \quantity{247}{km/h}\).
Alternatively…
Calculating individual components
The aeroplane’s component of velocity northward is \[v_1=300 \cos \alpha.\]
The wind subtracts from this a velocity component of \[v_2 = 60 \cos 30^\circ.\]
Hence we obtain \(v= v_1-v_2 =300 \cos 5.739 - 60 \cos 30 = 246.53... \approx \quantity{247}{km/h}\), as before.
Would a similar method also work for the first part of the problem?

