Can we show that $OAQY$ is a parallelogram?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

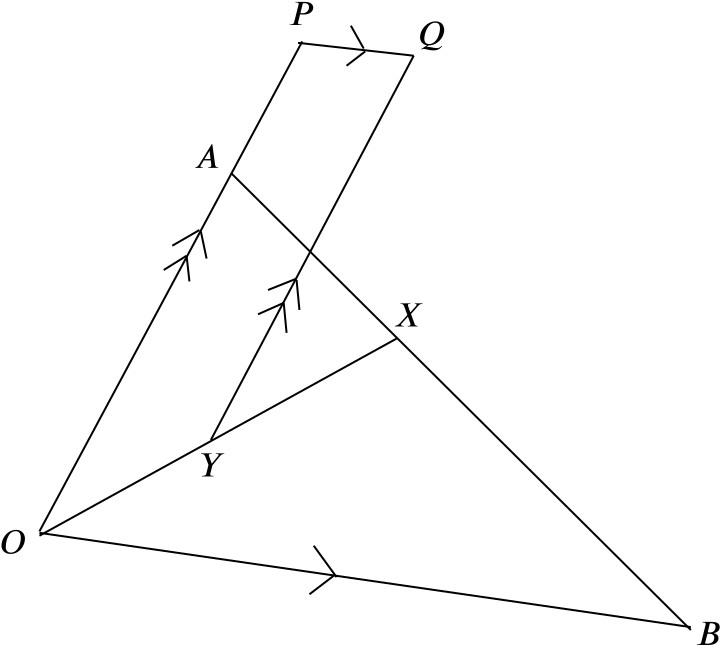
Note; this figure is not intended to be completely accurately drawn.

In the figure the points \(X\) and \(Y\) are such that \(AX = \dfrac{1}{2}XB\) and \(OY = YX\), while the point \(P\) is such that \(OA = 3AP\). The lines \(YQ\) and \(PQ\) are parallel to \(OA\) and \(OB\) respectively.

Given that \(\mathbf{OA} = \mathbf{a}\) and \(\mathbf{OB} = \mathbf{b}\), express \(\mathbf{OP}\) and \(\mathbf{OY}\) in terms of \(\mathbf{a}\) and \(\mathbf{b}\).

Given that \(\mathbf{YQ} = m\mathbf{a}\) and \(\mathbf{PQ} = n\mathbf{b}\), find the values of \(m\) and \(n\). Hence show that \(OAQY\) is a parallelogram.