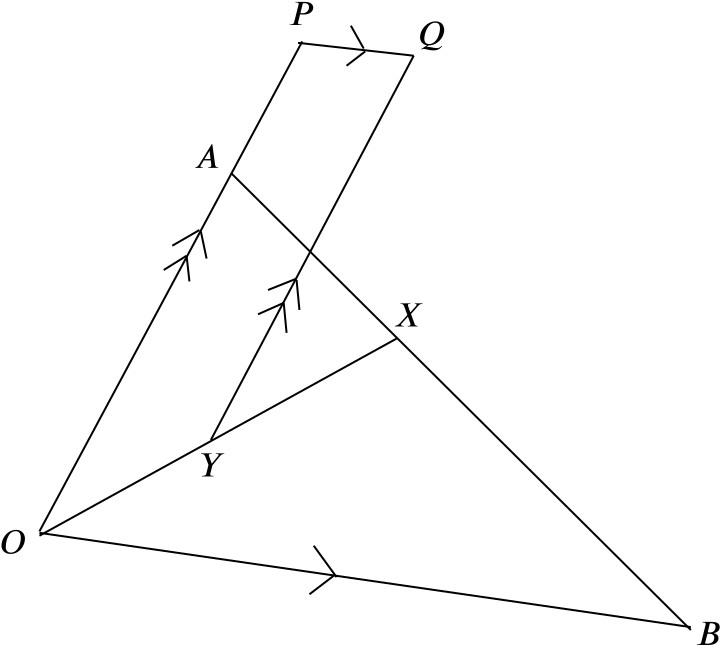
In the figure the points \(X\) and \(Y\) are such that \(AX = \dfrac{1}{2}XB\) and \(OY = YX\), while the point \(P\) is such that \(OA = 3AP\). The lines \(YQ\) and \(PQ\) are parallel to \(OA\) and \(OB\) respectively.
Given that \(\mathbf{OA} = \mathbf{a}\) and \(\mathbf{OB} = \mathbf{b}\), express \(\mathbf{OP}\) and \(\mathbf{OY}\) in terms of \(\mathbf{a}\) and \(\mathbf{b}\).
Since \(\mathbf{OA} = 3\mathbf{AP}\), we know \(\mathbf{OP}\) is \(\dfrac{4}{3}\mathbf{a}\).
We can see that the vector \[\mathbf{OX} = \mathbf{OA} + \mathbf{AX} = \mathbf{a} + \dfrac{1}{3}(\mathbf{b}-\mathbf{a}) = \dfrac{2}{3}\mathbf{a} + \dfrac{1}{3}\mathbf{b}.\]
We also have that the vector \[\mathbf{OY}=\dfrac{1}{2}\mathbf{OX} = \dfrac{1}{3}\mathbf{a} + \dfrac{1}{6}\mathbf{b}.\]
Given that \(\mathbf{YQ} = m\mathbf{a}\) and \(\mathbf{PQ} = n\mathbf{b}\), find the values of \(m\) and \(n\). Hence show that \(OAQY\) is a parallelogram.
The diagram tells us that \(\mathbf{OP} + \mathbf{PQ} = \mathbf{OY} + \mathbf{YQ}\).
Thus \[\dfrac{4}{3}\mathbf{a} + n\mathbf{b} = \dfrac{1}{3}\mathbf{a}+\dfrac{1}{6}\mathbf{b} + m\mathbf{a}.\]
Since \(\mathbf{a}\) and \(\mathbf{b}\) are linearly independent (they are not parallel) we can equate coefficients of \(\mathbf{a}\) and \(\mathbf{b}\) on either side of this equation.
We are effectively saying here that if \(\alpha \mathbf{a} + \beta \mathbf{b} = \gamma \mathbf{a} + \delta \mathbf{b},\) then \(\alpha = \gamma, \beta = \delta.\) Is that always true?
This tells us \[\dfrac{4}{3}= \dfrac{1}{3} + m \implies m = 1,\] and \[n =\dfrac{1}{6}.\]
Since \(m = 1\), we have that \(\big \vert \mathbf{AO} \big \vert= \big \vert\mathbf{QY}\big \vert\), and we know these two lines are parallel, so therefore \(OAQY\) is a parallelogram.

