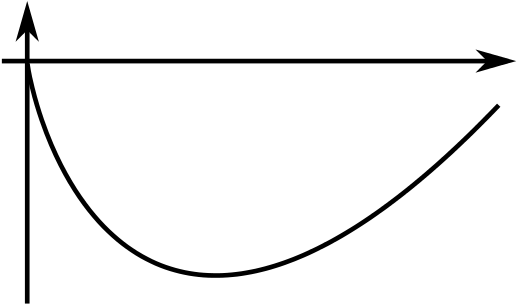
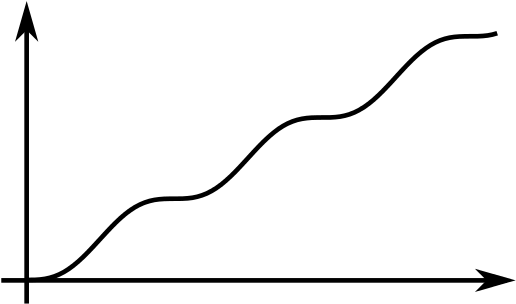
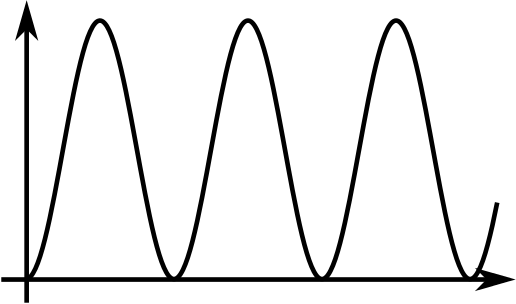
We have drawn the graphs of two functions, \(f(x)\) and \(g(x)\). In each case we have drawn the graph of the gradient function below the graph of the function.
Try to sketch the graph of the gradient function of the gradient function. You may find it helpful to think about how features of the function relate to features of its gradient function.
|
|

|
|
|

|
Notation
If we call our original function \(f(x)\) then
\(f'(x)\) denotes the gradient function, or first derivative, and we often say “\(f\) dash” or “\(f\) prime”
\(f''(x)\) denotes the gradient function of the gradient function, the second derivative, and we say “\(f\) double dash” or “\(f\) double prime”.
Similarly, if our function is called \(g(x)\) then we’d write \(g'(x)\) for the gradient function or first derivative and \(g''(x)\) for the second derivative.
Now compare your sketch of \(y=f''(x)\) with the graph of \(y=f(x).\) Do the same for \(y=g''(x)\) and \(y=g(x).\)
What do you notice?
How are features of the second derivative related to features of the original function?
Now try this
For each of the following functions
Sketch the graph of the function — what does it tell you about the first and second derivatives? Try to sketch these too (without doing any calculations).
Work out the first and second derivatives and amend your graphs if necessary — what do the first and second derivatives tell you about the original function?
\(f(x)=1-3x\)
\(g(x)=(x-1)(x+5)\)
\(h(x)=x^3-9x\)
\(k(x)=x+\dfrac{1}{x}\)

