If the trapezium rule is used to estimate the integral \[\int^1_0 f(x)\, dx,\] by splitting the interval \(0 \le x \le 1\) into \(10\) intervals then an overestimate of the integral is produced. It follows that
the trapezium rule with \(10\) intervals underestimates \(\int^1_0 2f(x)\, dx\);
the trapezium rule with \(10\) intervals underestimates \(\int^1_0 (f(x)-1)\, dx\);
the trapezium rule with \(10\) intervals underestimates \(\int^2_1 f(x-1)\, dx\);
the trapezium rule with \(10\) intervals underestimates \(\int^1_0 (1-f(x))\, dx\).
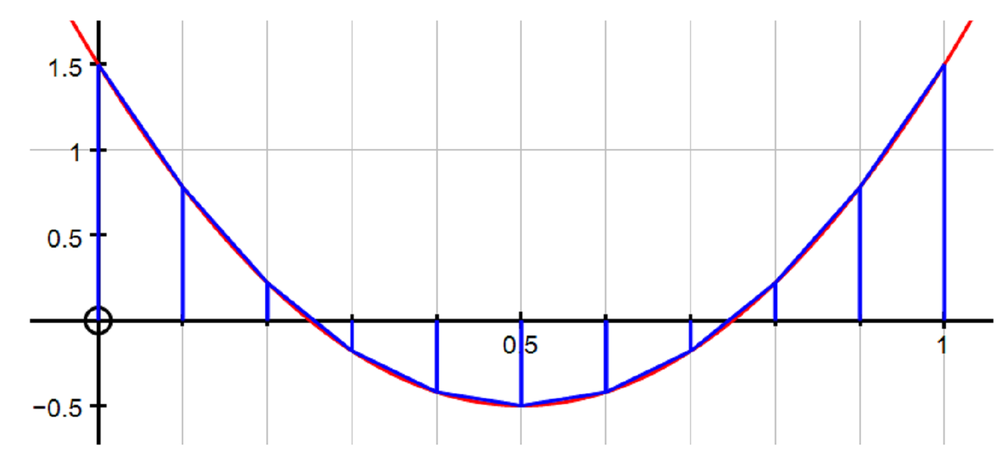
The trapezium rule is often used for finding the area under a curve approximately.
Here we’re asked to approximate the value of an integral with the trapezium rule, which is not quite the same thing.
The diagram shows a curve where the trapezium rule clearly overestimates when it’s above the \(x\)-axis.
When the curve is below the \(x\)-axis, the slanted edges of the trapezia lie above the curve, and therefore the trapezium rule gives a result that is larger than the actual integral (both the integral and the estimate are negative here).
You may need to think this through to convince yourself that this means the trapezium rule gives an overestimate when the curve lies below the \(x\)-axis.
In this example, every strip gives an overestimate; for some \(f(x)\), some strips may give underestimates that are outweighed by the overestimates.
Let’s call the overestimate of the first integral \(E\). Then
When estimating \(\int^1_0 2f(x)\; dx\), there will be an overestimate of \(2E\), since the graph has been stretched by a factor of two and so the areas from both the curve and the trapezia have been doubled.
When estimating \(\int^1_0 (f(x)-1)\; dx\), there will be an overestimate of \(E\), since the graph has been translated down by one, but the areas representing over/underestimates remain the same.
When estimating \(\int^2_1 f(x-1)\; dx\), there will be an overestimate of \(E\), since both the graph and the limits have simply been translated one to the right.
When estimating \(\int^1_0 (1-f(x))\; dx\), there will be an underestimate of \(E\), since the graph has first been reflected in the \(x\)-axis, which changes the overestimate into an underestimate, and then translated up by one, which does not change the areas representing the over/underestimates.
Hence the answer is (d).

