The graph \(y = f(x)\) of a certain function has been plotted below.
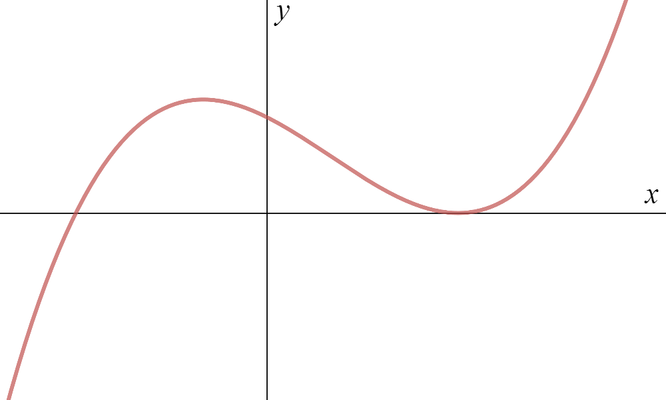
On the next three pairs of axes (A), (B), (C) are graphs of \[y = f(-x), \quad f(x-1), \quad -f(x)\] in some order. Say which axes correspond to which graphs.
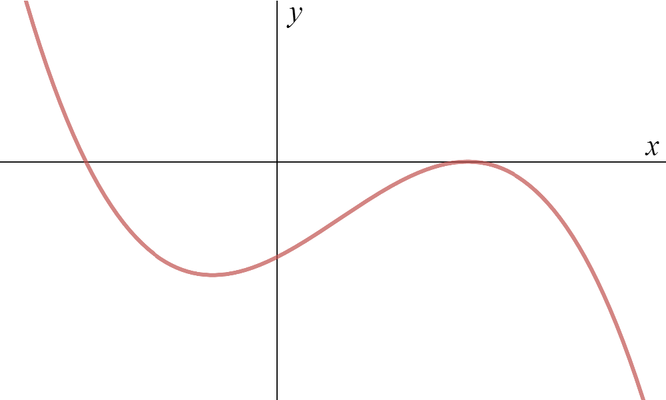
(A) 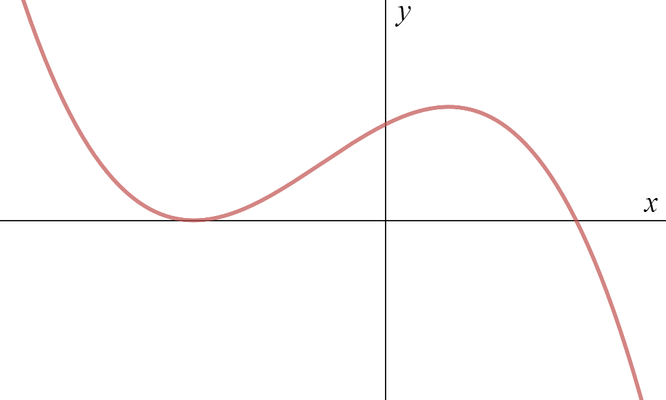
(B) 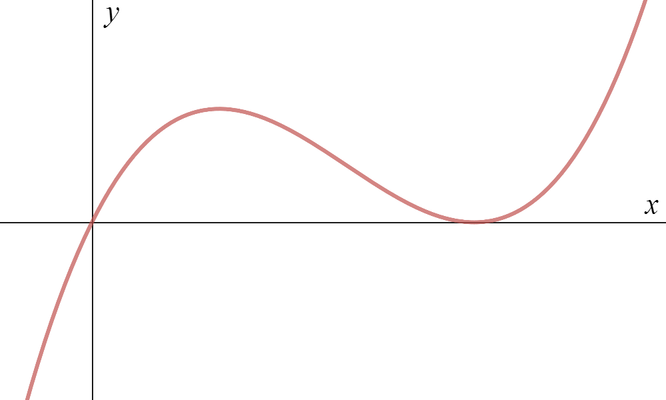
(C) Sketch graphs of both of the following functions \[y = 2^{-x^2} \quad \text{and} \quad y = 2^{2x - x^2}.\] Carefully label any stationary points.
Let \(c\) be a real number and define the following integral \[I(c) = \int^1_0 2^{-(x-c)^2} dx.\]
State the value(s) of \(c\) for which \(I(c)\) is largest. Briefly explain your reasoning. [Note you are not being asked to calculate this maximum value.]

