It is given that \[f(x)=(x-2)^2-\lambda(x+1)(x+2).\]
- Find the values of \(\lambda\) for which the equation \(f(x)=0\) has two equal roots.
and so \(\lambda = 0\) or \(\lambda=-48\).
- Show that, when \(\lambda=2\), \(f(x)\) has a maximum value of \(25\).
When \(\lambda=2\), we have \(f(x)=-x^2-10x\).
We find the maximum of \(f(x)\) by completing the square.
We can write \(f(x)=-(x+5)^2+25\), and since \(-(x+5)^2\) is strictly negative, we see that the maximum value of \(f(x)\) is \(25\), which occurs when \(x=-5\).
Alternatively we could find the derivative \(f'(x)\) and set this equal to zero to find the turning point.
Or we could find the roots of \(f(x)=0\), and use the symmetry of the parabola.
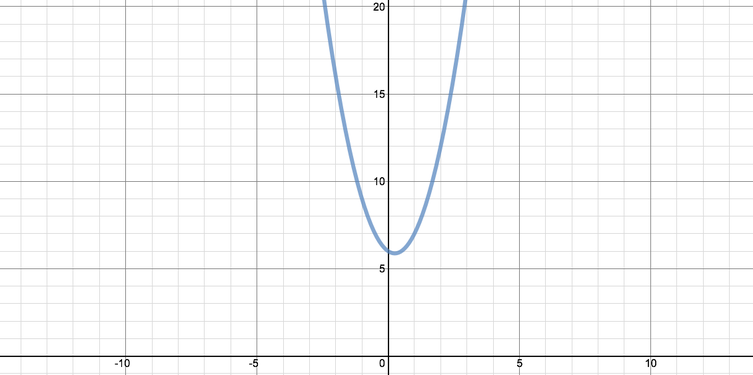
- Given that the curve \(y=f(x)\) has a turning point when \(x=\dfrac{1}{4}\), find the value of \(\lambda\) and sketch the curve for this value of \(\lambda\).
We have \[f'(x)=2(1-\lambda)x-(4+3\lambda).\]
We know that \(f'\left(\dfrac{1}{4}\right)=0\), since there is a turning point at \(x=\dfrac{1}{4}\).
So \[2(1-\lambda)\left(\frac{1}{4}\right)-4-3\lambda=0,\] and so \[1-\lambda-8-6\lambda=0,\] on multiplying the equation by \(2\). This simplifies to \(\lambda = -1\).
For this value of \(\lambda\), we have \(f(x)=2x^2-x+6\).
To sketch this graph we observe that the \(y\)-intercept is \(6\), and that \(x=\dfrac{1}{4}\) gives a minimum, since the coefficient of the \(x^2\) term is positive.
We calculate that \[f\left(\frac{1}{4}\right)=\frac{2}{16}-\frac{1}{4}+6=\frac{2-4+96}{16}=\frac{94}{16}=\frac{47}{8}.\]