For a positive whole number \(n\), the function \(f_{n}(x)\) is defined by \[f_{n}(x) = (x^{2n-1}-1)^2.\]
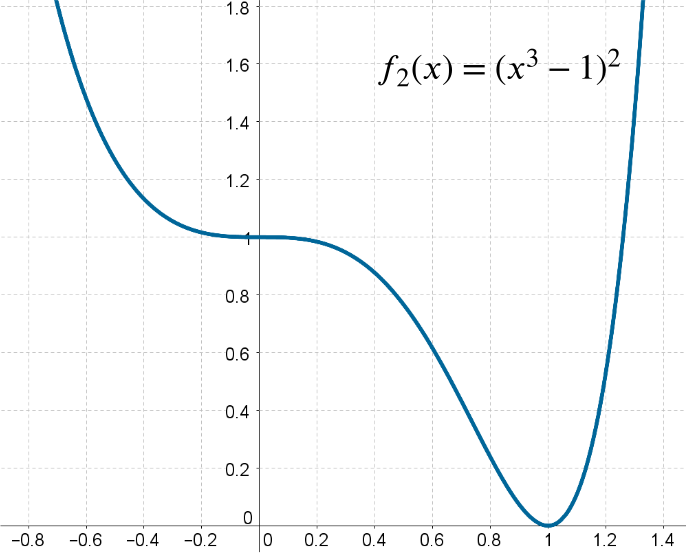
- Sketch the graph of \(y=f_{2}(x)\) labelling where the graph meets the axes.
We have \[f_{2}(x) = (x^3 - 1)^2 = x^6 - 2x^3 +1,\] so \(f_{2}(x)\) crosses the axes at \((1,0)\) and \((0,1)\).
Differentiating \(f_{2}(x)\) gives \[f'_{2}(x) = 6x^5 - 6x^2 = 6x^2(x^3 -1),\] so \(f'_{2}(x) = 0\) at \(x=0\) and \(x=1\). We have \(f'_{2}(x) \le 0\) for \(x<1\) and \(f'_{2}(x) > 0\) for \(x>1\).
Note that \(f_{2}(x)\) is large and positive for large positive and negative values of \(x\), and also that \(f_{2}(x) \ge 0\).
So \(f_{2}(x)\) must have a minimum at \(x=1\) and a point of inflection at \(x=0\).
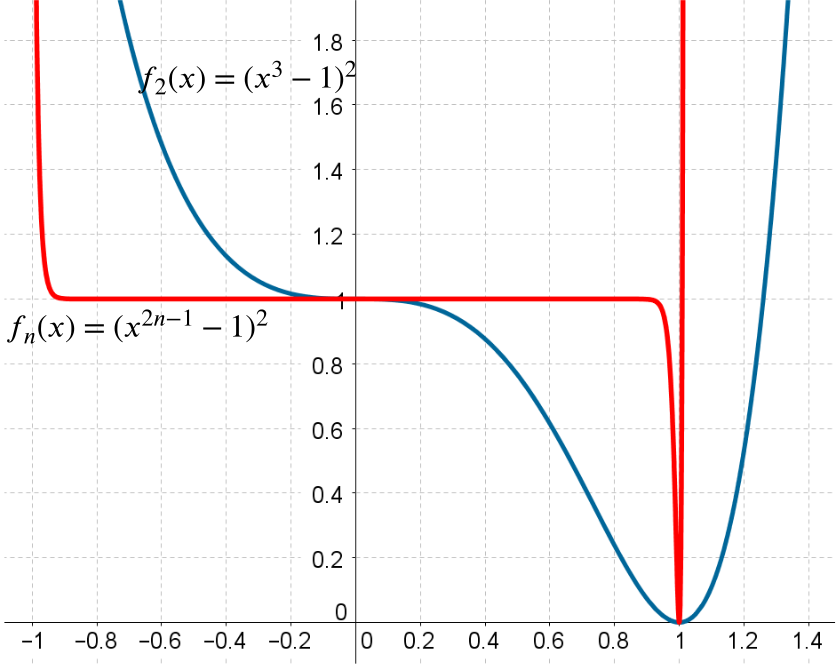
- On the same axes sketch the graph of \(y=f_{n}(x)\) where \(n\) is a large positive integer.
The function \(f_{n}(x)\) still crosses the axes at \((1,0)\) and \((0,1)\), and is large and positive for large positive and negative values of \(x\).
Also, as \(x^{2n-1}-1\) is very close to \(-1\) for \(-1<x<1\), \(f_{n}(x)\) is close to \(1\) in this range.
- Determine \[\int_0^1 \! f_{n}(x) \, \mathrm{d}x.\]
\[\int_0^1 \! f_{n}(x) \, \mathrm{d}x = \int_0^1 \! (x^{2n-1}-1)^2 \, \mathrm{d}x = \int_0^1 \! (x^{4n-2} - 2x^{2n-1} + 1) \, \mathrm{d}x = \frac{1}{4n-1} - \frac{1}{n} + 1.\]
The positive constants \(A\) and \(B\) are such that \[\int_0^1 \! f_{n}(x) \, \mathrm{d}x \le 1 - \frac{A}{n+B} \quad \text{for all $n \ge 1$}.\]
Show that \[(3n-1)(n+B) \ge A(4n-1)n,\] and explain why \(A \le \dfrac{3}{4}\).
We can be sure that multiplying through by the denominators doesn’t change the direction of the inequality because the denominators are all positive.
Expanding this and collecting powers of \(n\) gives
\[(3-4A)n^2 + (A+3B-1)n - B \ge 0 \quad \text{for $n\ge1$} \]
The left-hand side is a quadratic in \(n\), which we want to be non-negative for all values of \(n \ge 1\).
Graphically this says that we want the parabola described by this quadratic to lie above the \(n\)-axis when \(n \ge 1\):
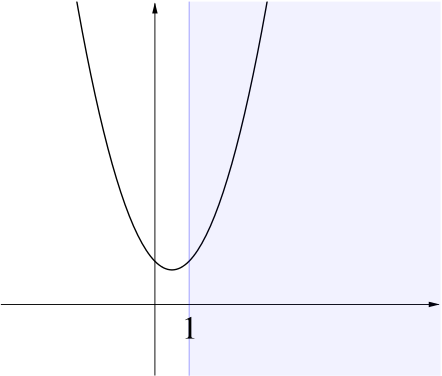
We see that a necessary condition is that the parabola is vertex-down, which requires the coefficient of \(n^2\) to be non-negative.
Hence we deduce that \(3 -4A \ge 0\), that is, \(A \le \dfrac{3}{4}\).
- When \(A=\dfrac{3}{4}\), what is the smallest possible value of \(B\)?
When \(A=\dfrac{3}{4}\), the \(n^2\) term in the inequality disappears, and it becomes
\[(12B-1)n-4B \ge 0 \quad \text{for $n\ge1$}.\]
The graph of the left-hand side against \(n\) is a straight line. The inequality says that we want this line to lie above the \(n\)-axis for all \(n \ge 1\):
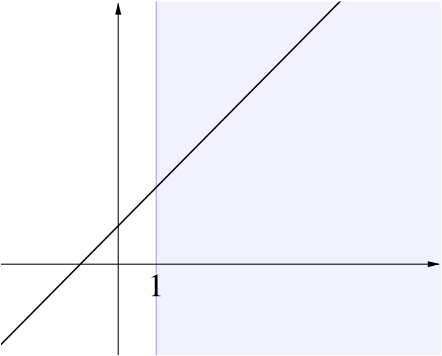
This will happen if and only if the gradient is non-negative, and the value at \(n=1\) is non-negative, that is, \(12B-1 \ge 0\) and \(12B-1-4B \ge 0\).
Rearranging these inequalities for \(B\) gives \(B \ge \dfrac{1}{12}\) and \(B \ge \dfrac{1}{8}\). So the smallest possible value of \(B\) is \(\dfrac{1}{8}\).

