Can we show that the area of this hexagon is $2(x^2 + xy + y^2)$?
Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Ref: R8987

Printable/supporting materials Printable version Fullscreen mode Teacher notes

Question

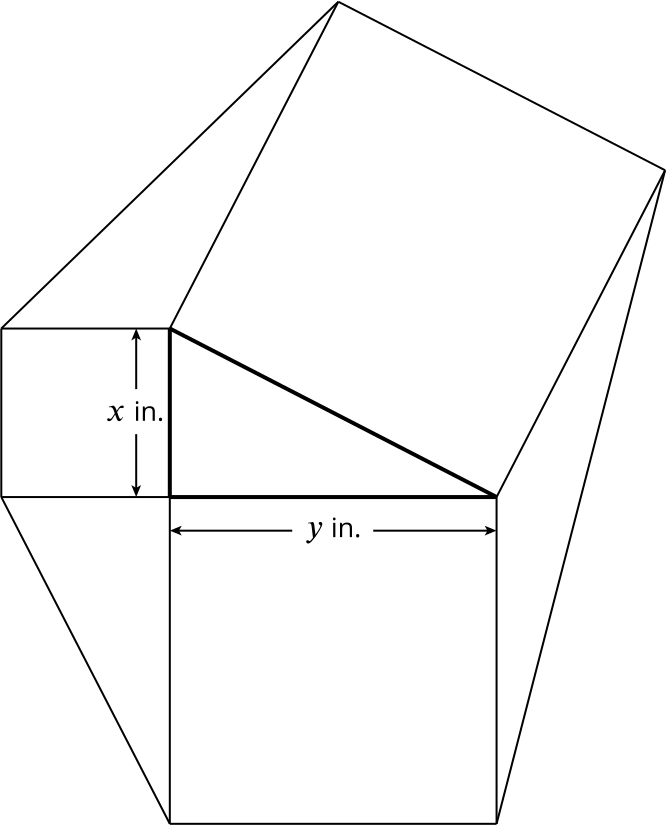
Diagram of a right-angled triangle, with the constructed squares and the resulting hexagon.

The lengths of the two smaller sides of a right-angled triangle are $x$ in. and $y$ in. A square is constructed on each side of the triangle and the exterior points of the squares are joined to form a hexagon as in the diagram above. Show that the area of the hexagon is $2(x^2 + xy + y^2)$ sq. in. Given that $x + y = 10$, determine the minimum area of the hexagon.

Previous Next

Calculus meets Functions

Can we show that the area of this hexagon is $2(x^2 + xy + y^2)$? Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Question

Station

Lines

Can we show that the area of this hexagon is $2(x^2 + xy + y^2)$?
Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource