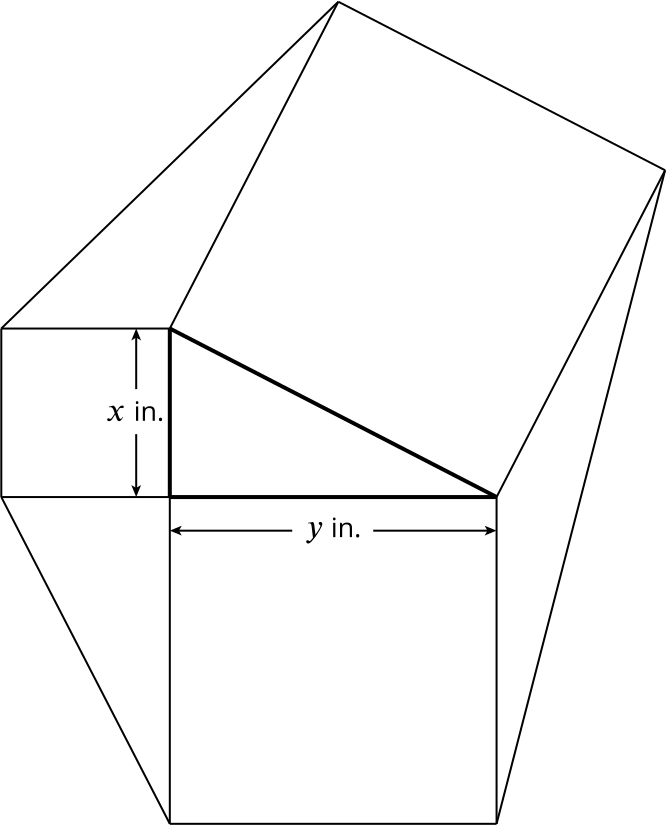
The lengths of the two smaller sides of a right-angled triangle are \(x\) in. and \(y\) in. A square is constructed on each side of the triangle and the exterior points of the squares are joined to form a hexagon as in the diagram above. Show that the area of the hexagon is \(2(x^2 + xy + y^2)\) sq. in.
The area, \(A\), of the hexagon is the sum of the seven constituent parts that are labelled in the diagram below. We have also labelled some angles.
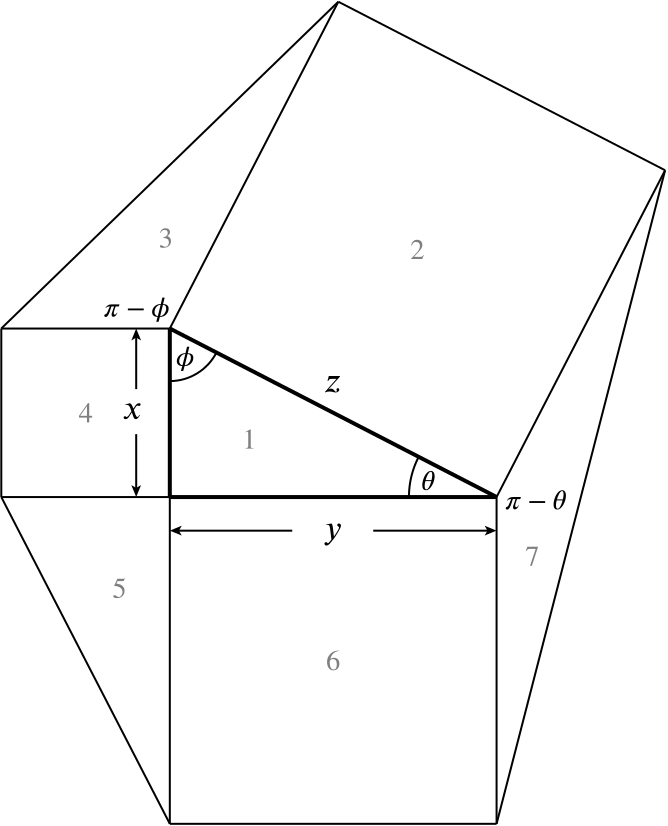
We need to express \(A_{2}\) in terms of \(x\) and \(y\). By Pythagoras’ theorem, \(x^2 + y^2 = z^2\), so \(A_{2}=x^2+y^2\).
We still need to find \(A_3\) and \(A_{7}\) in terms of \(x\) and \(y\).
If a triangle has an angle of size \(\alpha\) with adjacent sides of lengths \(a\) and \(b\), its area is \(\dfrac{1}{2} ab \sin \alpha\).
We also have that \(\sin(\pi - \phi) = \sin \phi\) and we can write \(\sin \phi\) as \(\dfrac{y}{z}.\) Similarly, \(\sin(\pi-\theta)=\dfrac{x}{z}\).
Consequently, \[\begin{equation*} A_3 = \frac{1}{2} x z \sin(\pi - \phi) = \frac{1}{2} x z \sin \phi = \frac{1}{2} x z \dfrac{y}{z} = \frac{xy}{2}. \end{equation*}\] Similarly, \[\begin{equation*} A_7 = \frac{1}{2} y z \sin(\pi - \theta) = \frac{1}{2} y z\sin \theta = \frac{1}{2} y z\dfrac{x}{z} =\frac{xy}{2}. \end{equation*}\] Thus, the area of the hexagon is \[\begin{equation*} A = A_{1}+A_{2}+\cdots+A_{7} = \frac{xy}{2} + (x^2 + y^2) + \frac{xy}{2} + x^2 + \frac{xy}{2} + y^2 + \frac{xy}{2} = 2(x^2 + xy + y^2) \end{equation*}\]as required.
Given that \(x + y = 10\), determine the minimum area of the hexagon.
As \(\dfrac{d^2A}{dx^2}>0\), any stationary point is, indeed, a minimum.
We have shown that \[\begin{equation*} \frac{dA}{dx} = 0 \iff x = 5, \end{equation*}\] so it follows that the minimum area is attained when \(x = 5\) and \(y = 10 - x = 5\). Hence, the minimum area is \[\begin{equation*} 2(5^2 + 5^2 + 5^2) = 2 \times 75 = 150 \,\,\,\text{sq. in.} \end{equation*}\]
