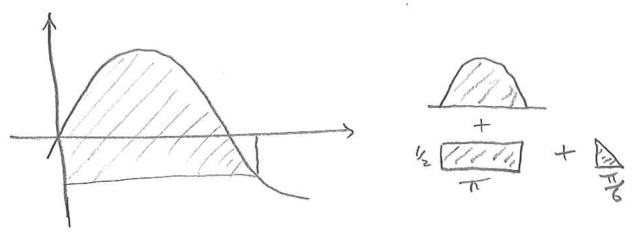
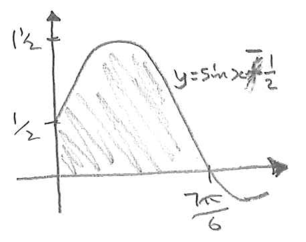
An exam question showed this diagram of the curve \(y=\sin x\).

How could we work out the area of the shaded region?
Which of the following expressions will give the shaded area? Make sure you can explain why each one does or does not.
\[\int_0^\frac{7\pi}{6} \sin x\,dx\]
\[\int_0^\pi \sin x\,dx+\pi\times\frac{1}{2}+\frac{1}{2}\times\frac{1}{2}\times\frac{\pi}{6}\]
\[\int_0^\frac{7\pi}{6} \sin x+\frac{1}{2}\,dx\]
\[\int_0^\pi \sin x\,dx+\frac{7\pi}{6}\times\frac{1}{2}-\int_\pi^\frac{7\pi}{6} \sin x\,dx\]
\[\int_0^\frac{7\pi}{6} \sin x-\frac{1}{2}\,dx\]
\[\int_0^\pi \sin x\,dx+\frac{7\pi}{6}\times\frac{1}{2}+\int_\pi^\frac{7\pi}{6} \sin x\,dx\]
\[\int_0^\pi \sin x\,dx+\pi\times\frac{1}{2}+\int_0^\frac{\pi}{6} \sin x\,dx\]
\[\int_0^\pi \sin x\,dx+\frac{7\pi}{6}\times\frac{1}{2}-\int_0^\frac{\pi}{6} \sin x\,dx\]
\[\frac{7\pi}{6}\times\frac{3}{2}-\int_0^\frac{7\pi}{6} 1-\sin x\,dx\]
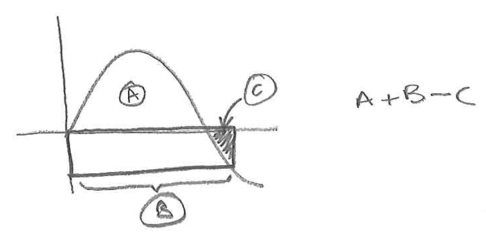
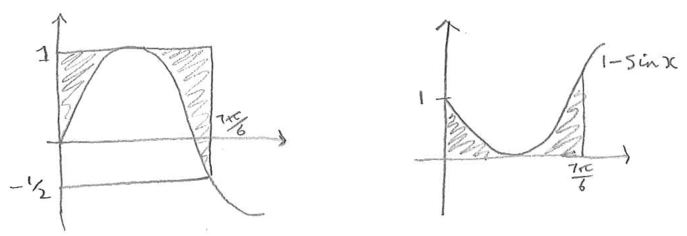
Here are some sketches made by students while working on this question. Which expressions do they go with?