An exam question showed this diagram of the curve \(y=\sin x\).

How could we work out the area of the shaded region?
There are essentially three methods used in these examples to calculate the shaded area.
- We can break the shaded area into pieces and calculate the area of each piece. This is illustrated in sketches (A) and (B).
- We can transform the graph so that we have a simple integral to perform. This appears in sketch (C).
- We can start with a large rectangle and use a transformation to subtract the unwanted area, as in sketch (D).
\[\int_0^\frac{7\pi}{6} \sin x\,dx\]
This integral tells us about the area between the curve and the \(x\)-axis but we want to know the area between the curve and the line \(y=-\frac{1}{2}\).
\[\int_0^\frac{7\pi}{6} \sin x+\frac{1}{2}\,dx\]
\[\int_0^\frac{7\pi}{6} \sin x-\frac{1}{2}\,dx\]
These integrals are attempting the transformation method shown in sketch (C). The curve needs to be translated vertically upwards so expression (3) is correct.

From the graph of \(\cos x\) or the unit circle we know that \[\cos\frac{7\pi}{6}=-\cos\frac{\pi}{6}=-\frac{\sqrt{3}}{2}\] and so the shaded area is \[\frac{\sqrt{3}}{2}+\frac{7\pi}{12}+1\approx3.70.\]
\[\int_0^\pi \sin x\,dx+\pi\times\frac{1}{2}+\frac{1}{2}\times\frac{1}{2}\times\frac{\pi}{6}\]
\[\int_0^\pi \sin x\,dx+\pi\times\frac{1}{2}+\int_0^\frac{\pi}{6} \sin x\,dx\]
These expressions are attempts to use the decomposition method shown in sketch (A).
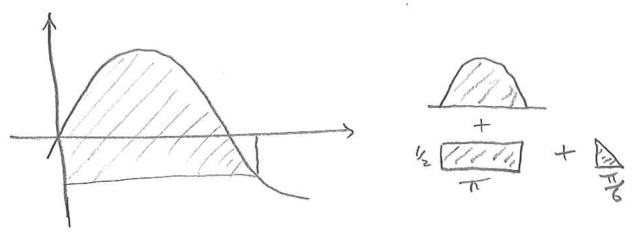
They correctly evaluate the area of the loop above the axis and the rectangle below it. Expression (2) treats the small area at the right as a triangle. This would give a result which is close but not correct since the graph is actually curved.
Expression (7) uses the fact that the areas between the curve and the axis are the same for the regions \(0\le x\le\frac{\pi}{6}\) and \(\pi\le x\le\frac{7\pi}{6}\). However, this gives us the area on the wrong side of the curve. Again, the result is close but not correct.
How could we modify expression (7) to make it give the correct area?
\[\int_0^\pi \sin x\,dx+\frac{7\pi}{6}\times\frac{1}{2}-\int_\pi^\frac{7\pi}{6} \sin x\,dx\]
\[\int_0^\pi \sin x\,dx+\frac{7\pi}{6}\times\frac{1}{2}+\int_\pi^\frac{7\pi}{6} \sin x\,dx\]
\[\int_0^\pi \sin x\,dx+\frac{7\pi}{6}\times\frac{1}{2}-\int_0^\frac{\pi}{6} \sin x\,dx\]
These are attempts to use the decomposition method shown in sketch (B).
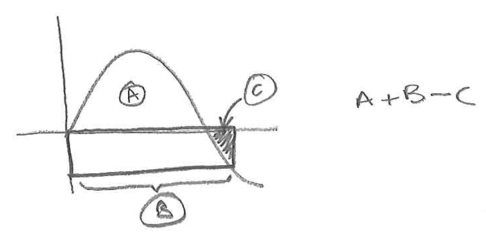
They correctly evaluate the area of the loop above the axis and of the wide rectangle below the axis. To find the shaded area we then need to subtract the area above the curve at the right (labelled as C in this student’s sketch).
The integral from \(\pi\) to \(\frac{7\pi}{6}\) tells us this area but the value of the integral is negative since the curve is below the axis here. So we have to add the integral as in expression (6).
Expression (8) again uses the fact that the area between \(0\) and \(\frac{\pi}{6}\) is the same as the area we need to subtract.
Can you simplify expression (6) so it contains only one integral? How does this simplified version relate to the transformation method in expression (3)?
Evaluate one or other of these correct expressions to check they give the same shaded area as we calculated above.
\[\frac{7\pi}{6}\times\frac{3}{2}-\int_0^\frac{7\pi}{6} 1-\sin x\,dx\]
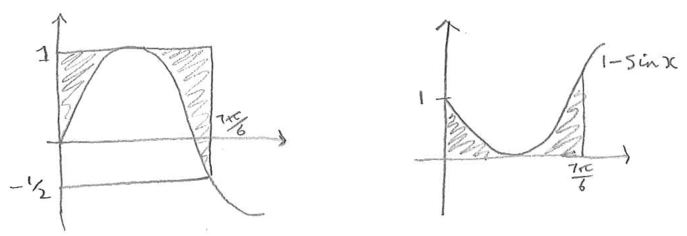
Here we take the bounding rectangle and subtract the area we don’t want, which is shaded in sketch (D). It is the same as the area under \(y=1-\sin x\).
Evaluate this expression to check it gives the same result as we calculated above.
Summary
| Correct expressions | Incorrect expressions | Student’s sketch |
|---|---|---|
| (1) | ||
| (3) | (5) | (C) |
| (2), (7) | (A) | |
| (6), (8) | (4) | (B) |
| (9) | (D) |

