What can we say if a normal to an ellipse passes through this point?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Implicitly differentiating the equation of the ellipse with respect to \(x\), we find \[\frac{2x}{a^2} + \frac{2y}{b^2} \frac{dy}{dx} = 0\] and therefore \[\begin{align*} \frac{dy}{dx} &= - \frac{b^2x}{a^2y} \\ &= - \frac{b^2 a \cos \theta}{a^2 b \sin \theta} \\ &= - \frac{b \cos \theta}{a \sin \theta}. \end{align*}\]

Since the normal is perpendicular to the tangent, it has slope \[m = -\frac{1}{dy/dx} = \frac{a \sin \theta}{b \cos \theta}.\]

Hence the equation of the line is \[y - b\sin\theta = \frac{a \sin \theta}{b \cos \theta}\left(x - a \cos \theta\right)\] which we can rearrange to obtain \[a^2 - b^2 = \frac{ax}{\cos \theta} - \frac{by}{\sin\theta}\] as required.

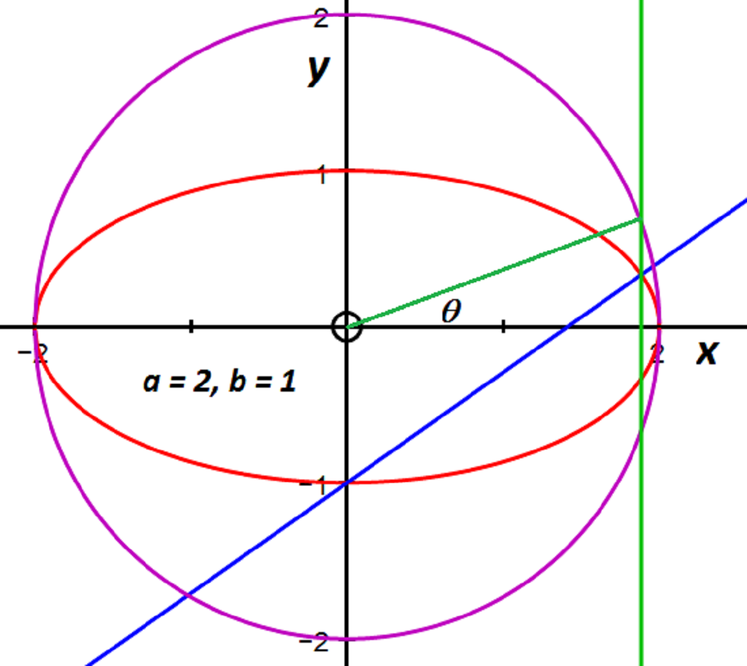
The minor axis is the shortest diameter of the ellipse (a diameter of the ellipse is a chord that passes through the centre).

The ends have coordinates \((0,\pm b)\) (assuming that \(a \geq b>0\), which we can say without loss of generality).

If we know there is a value of \(\theta\) between \(0\) and \(\pi/2\) such that the normal at \(P\) passes through one end of the minor axis, then from the diagram, this normal must pass through \((0, -b)\).

Substituting \((0,-b)\) into the equation of the normal gives \[a^2 - b^2 = \frac{b^2}{\sin\theta} \qquad \implies \qquad \left(\frac{a}{b}\right)^2 = 1 +\frac{1}{\sin\theta}.\]

But now since \(0 < \sin\theta < 1\) we conclude \[\left(\frac{a}{b}\right)^2 > 2 \qquad \implies \qquad \frac{b^2}{a^2} < \frac{1}{2}.\]

If an ellipse is a ‘squashed’ circle, then the eccentricity measures the degree of ‘squashedness’. We have the standard result that \(e = \sqrt{1-\dfrac{b^2}{a^2}}\).

In our case, the eccentricity \[ e = \sqrt{1-\frac{b^2}{a^2}} > \sqrt{1 - \frac 1 2} = \frac{1}{\sqrt{2}} \] as required.