The point \(S\) is a focus of the ellipse \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\), and \(P\) is a point on the ellipse such that \(PS\) is perpendicular to the axis of \(x\). The tangent and normal to the ellipse at \(P\) meet the axis of \(y\) in \(Q\) and \(R\) respectively. If \(H\) is the other focus of the ellipse prove that \(QR=HP\).
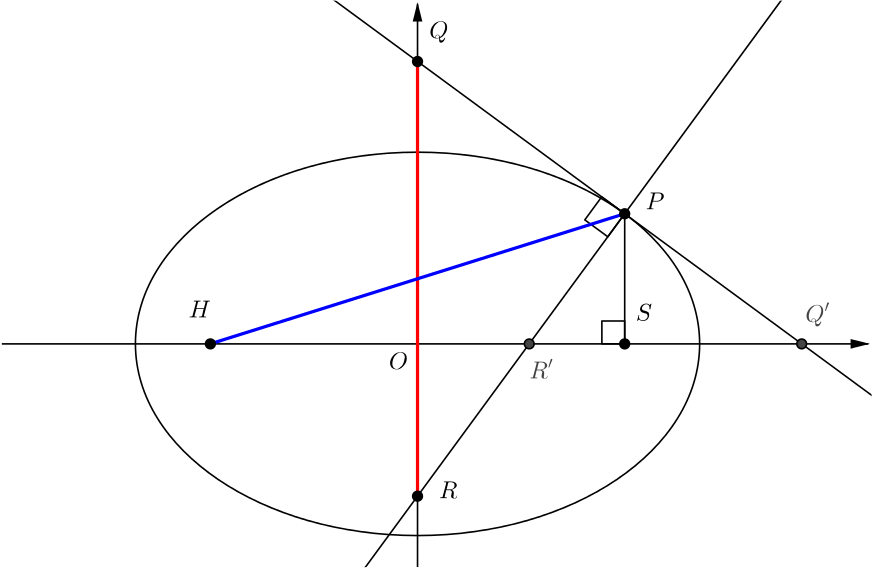
We’ve added points \(Q'\) and \(R'\), where \(Q'\) and \(R'\) are the points at which the tangent and normal intersect the \(x\) axis.
We’ll use the reflection property of the ellipse. This states that any light beam sent from one focus will always reflect back to the other focus.
In our diagram, this is equivalent to the statement that \(\angle HPQ = \angle Q'PS\).
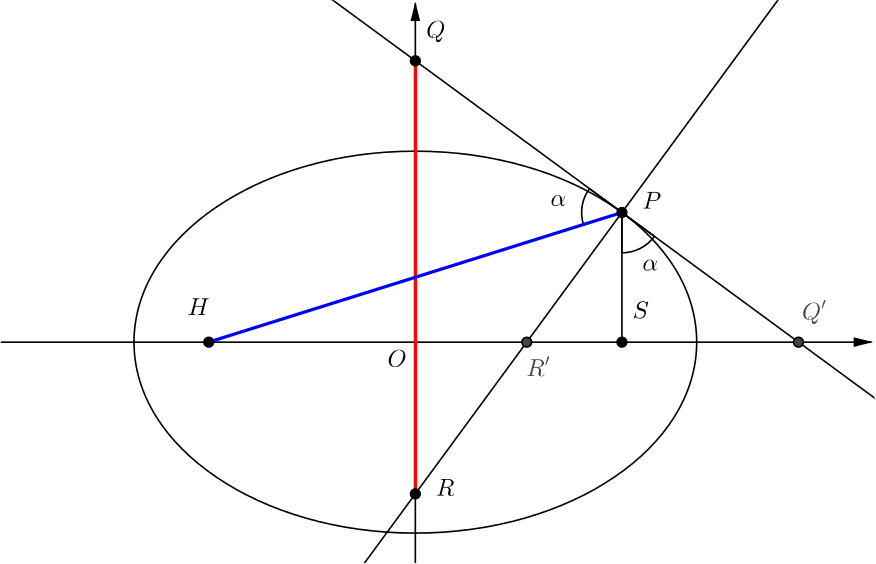
Let this angle be \(\alpha\) and let \(\beta=90^\circ-\alpha\), so that any right-angled triangle for which one angle is either \(\alpha\) or \(\beta\) must have angles \(\alpha\), \(\beta\) and \(90^\circ\) (as they must sum to \(180^\circ\)).
We can now find most of the angles in the diagram.
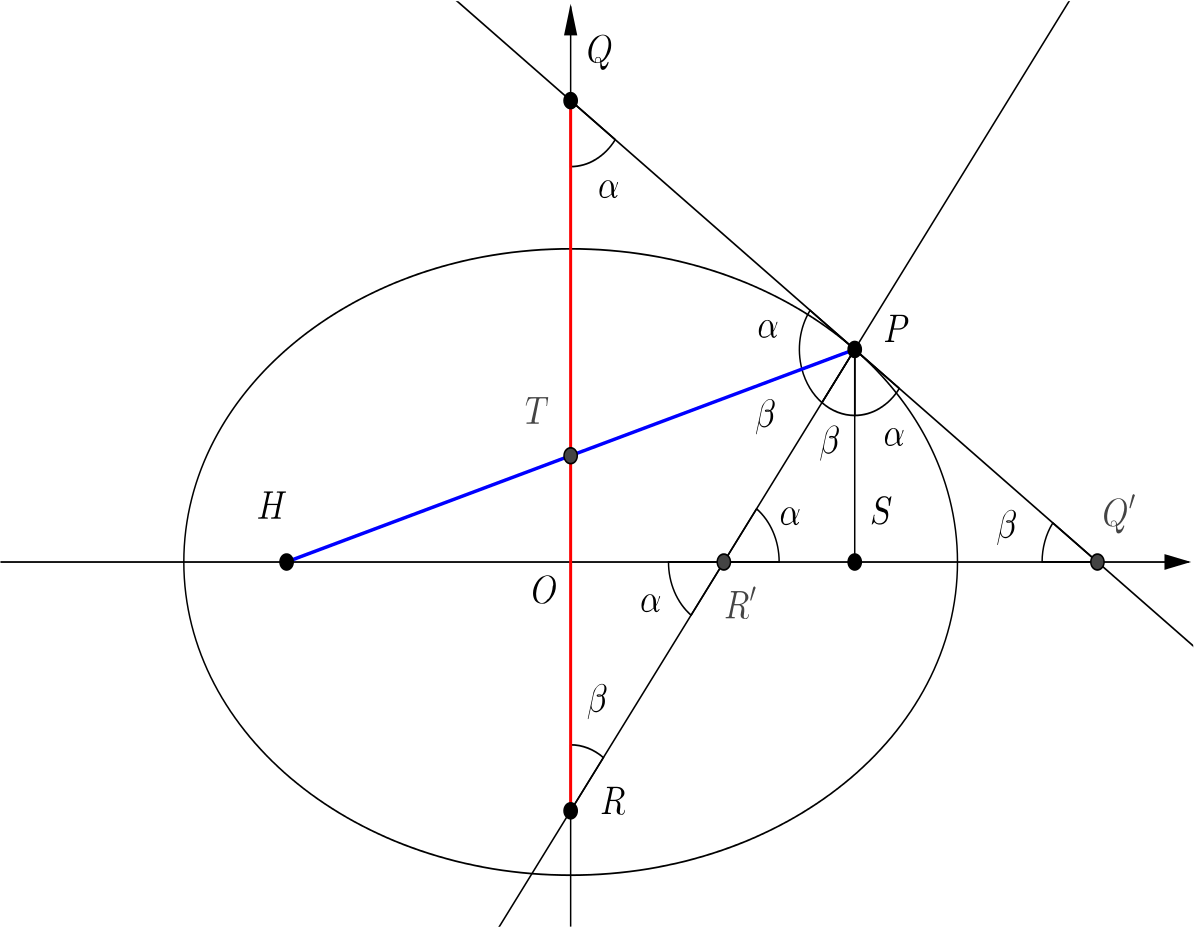
We can see that \(\triangle QTP\) and \(\triangle PTR\) are both isosceles. This tells us that \(QT=TP\) and \(TP=TR\) and so \(QT=TP=TR\).
As the foci are equidistant from the minor axis, we know that the \(x\)-axis bisects \(HS\), and so must also bisect \(HP\).
Hence \(HT=TP\), which gives us that \(QR=QT+TR=2TP = HT+TP=HP\), as required.
What can we deduce about the quadrilateral \(PQHR\)?
As an extension, show that \(TS=TP\). What can we deduce about the polygon \(PQHRS\)?
Does this result still hold when \(P\) is any point on the ellipse?

