The point \(S\) is a focus of the ellipse \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\), and \(P\) is a point on the ellipse such that \(PS\) is perpendicular to the axis of \(x\). The tangent and normal to the ellipse at \(P\) meet the axis of \(y\) in \(Q\) and \(R\) respectively. If \(H\) is the other focus of the ellipse prove that \(QR=HP\).
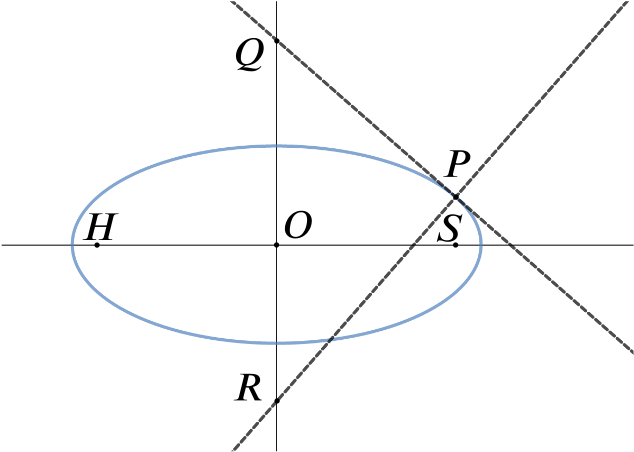
Firstly, we can work out the coordinates of \(P\).
so \[y^2 = \frac{b^4}{a^2}\] and so \[y = \frac{b^2}{a},\] since we have picked \(P\) to be in the top right quadrant. Thus \(P\) has coordinates \(\left(\sqrt{a^2-b^2},\dfrac{b^2}{a}\right)\).
Now let’s work out the equation of the tangent to the ellipse at \(P\).
The equation of the tangent to the ellipse through \(P\) therefore has the equation \[y-\frac{b^2}{a}=-\frac{\sqrt{a^2-b^2}}{a}\left(x-\sqrt{a^2-b^2}\right).\]
We can use this equation to work out the coordinates of \(Q\).
so \(Q\) has coordinates \((0,a)\). (Without loss of generality we are assuming \(a>b>0\).)
Now let’s work out the equation of the normal at \(P\) and the coordinates of \(R\).
so \(R\) has coordinates \(\left(0,\dfrac{b^2-a^2}{a}\right)\).
Now we want to prove that \(QR = HP\).
The other focus of the ellipse, \(H\), has coordinates \(\left(-\sqrt{a^2-b^2},0\right)\).
Therefore we have \[\begin{align*} HP &= \sqrt{(2\sqrt{a^2-b^2})^2+\left(\frac{b^2}{a}\right)^2} \\ &= \sqrt{4(a^2-b^2)+\frac{b^4}{a^2}}\\ &= \frac{1}{a}\sqrt{4a^4-4a^2b^2+b^4} \\ &= \frac{1}{a}\sqrt{(2a^2-b^2)^2}=\frac{2a^2-b^2}{a}. \end{align*}\]Similarly, \[QR = a+\frac{a^2-b^2}{a}=\frac{2a^2-b^2}{a}\] since we know that \(Q\) is above the \(x\)-axis and \(R\) is below it (had we chosen the other focus as \(S\) this would be reversed.)
Thus \(QR = HP\) as required.
For an alternative solution using the geometry of the ellipse, look at Solution 2.

