Here are some examples for you to try your ideas out on. For each set of three points, find the equation of the circle passing through them.
It is certainly worth sketching a graph to help you understand what is going on in each case!
Which of your approaches is the most effective?
\(A(3,2)\), \(B(3,6)\), \(C(5,8)\)
\(A(0,4)\), \(B(4,0)\), \(C(-6,0)\)
\(A(-1,-5)\), \(B(-2,2)\), \(C(2,-1)\)
\(A(3,3)\), \(B(1,-2)\), \(C(4,1)\)
Brief answers
\((x-7)^2+(y-4)^2=20\)
\((x+1)^2+(y+1)^2=26\)
\(\left(x+\frac{3}{2}\right)^2+\left(y+\frac{3}{2}\right)^2= \frac{25}{2}\)
\(\left(x-\frac{7}{6}\right)^2+\left(y-\frac{5}{6}\right)^2= \frac{145}{18}\)
Full solutions
- \(A(3,2)\), \(B(3,6)\), \(C(5,8)\)
A geometric approach
In the suggestion, we saw that the centre of the circle must be the same distant from \(A\) and \(B\), and it turns out that those points which are lie on the perpendicular bisector of the line segment \(AB\).
So if we draw the perpendicular bisector of \(AB\), the circle’s centre must lie on it.
Likewise, if we draw the perpendicular bisector of \(AC\) or of \(BC\), the circle’s centre must lie on that, too.
The point where these perpendicular bisectors meet must therefore be the centre of the circle through the points \(A\), \(B\) and \(C\).
This GeoGebra applet shows how this works for this question; you can move the points \(A\), \(B\) and \(C\) if you wish.
We can now see that the perpendicular bisector of \(AB\) is going to be the line \(y=4\) since \(A\) and \(B\) have the same \(x\)-coordinate.
The perpendicular bisector of the chord \(BC\) passes through the midpoint of \(BC\), which is \((4,7)\). (The midpoint of a line between two points can be found by averaging the coordinates of the two points: its coordinates are half way between the coordinates of \(B\) and \(C\).)
The gradient of line through the points \(B\) and \(C\) is \[m=\frac{8-6}{5-3}=\frac{2}{2}=1,\] so the gradient of the line perpendicular to that is \[m'=-\frac{1}{m}=-\frac{1}{1}=-1\] (the negative reciprocal of \(m\)).
The equation of this second perpendicular bisector is therefore \[\begin{align*} &&y-7&=-(x-4)&&\quad \\ \implies&& y&=11-x. \end{align*}\]We now need to find the point of intersection of these two lines as this is the centre of our circle. Solving the equations \(y=4\) and \(y=11-x\) simultaneously gives the coordinates of their intersection, which is \(O(7,4)\). Finally, we want the radius of our circle so we work out the length \(|OA|\): \[r=|OA|=\sqrt{(3-7)^2+(2-4)^2}=\sqrt{20}.\] Therefore the equation of the circle is \[(x-7)^2+(y-4)^2=20.\]
Incidentally, note that as the equation for the circle only needs \(r^2\) and not \(r\) itself, we could have found \(r^2=|OA|^2\) and dispensed with all square roots. We will do this from now on in this question.
An algebraic approach
Following the suggestion, we substitute for \(x\) and \(y\) in the equation \((x-a)^2+(y-b)^2=r^2\) for our three coordinates to find \(a\), \(b\) and \(r\). This gives us the following three simultaneous equations: \[\begin{align} (3-a)^2+(2-b)^2&=r^2 \label{eq:1}\\ (3-a)^2+(6-b)^2&=r^2 \label{eq:2}\\ (5-a)^2+(8-b)^2&=r^2 \label{eq:3} \end{align}\] In this form, they are not that easy to solve, so we expand the brackets: \[\begin{align} \eqref{eq:1} \implies && a^2-6a+b^2-4b+13&=r^2&&\quad \label{eq:4}\\ \eqref{eq:2} \implies && a^2-6a+b^2-12b+45&=r^2 \label{eq:5}\\ \eqref{eq:3} \implies && a^2-10a+b^2-16b+89&=r^2 \label{eq:6} \end{align}\] Now subtracting any pair of these eliminates all of the square terms, as follows: \[\begin{align*} \eqref{eq:5}-\eqref{eq:4}& \implies -8b+32=0 \implies b=4\\ \eqref{eq:6}-\eqref{eq:5}& \implies -4a+44-4\times 4 \implies a=7 \end{align*}\] Substituting our values for \(a\) and \(b\) into \(\eqref{eq:1}\) we find the value of \(r^2\): \[\begin{align*} r^2&=(3-7)^2+(2-4)^2 \\ &=16+4=20. \end{align*}\]Therefore the equation of the circle is \[(x-7)^2+(y-4)^2=20.\]
Which method is quicker/easier here?
By virtue of the fact we can write down one of the perpendicular bisectors by inspection, probably the geometric method here.
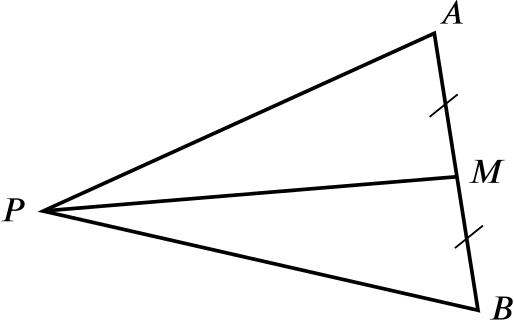
- \(A(0,4)\), \(B(4,0)\), \(C(-6,0)\)
Geometric, perpendicular bisector method
The midpoint of \(AB\) is \((2,2)\), so the perpendicular bisector passes through this point. The gradient of \(AB\) is \(-1\), so the perpendicular bisector has gradient \(-1/-1=1\) and thus the equation of the perpendicular bisector is \[y-2=1(x-2) \implies y=x,\] as is apparent from the sketch. Similarly, the perpendicular bisector of the chord \(BC\) is the line \(x=-1\). Thus the point of intersection, and the centre of the circle, is \(O(-1,-1)\). We work out the length \(|OA|\) to find the (square of the) radius: \[r^2 = |OA|^2 = (-1-0)^2+(-1-4)^2=26\] so the equation of our circle through the points \(A\), \(B\) and \(C\) is \[(x+1)^2+(y+1)^2=26.\]
Algebraic, simultaneous equations method
Substituting the coordinates \(A\), \(B\) and \(C\) into the general equation for a circle and expanding the brackets as in part (a), we find \[\begin{align} a^2+b^2-8b+16 &=r^2 \label{eq:7}\\ a^2-8a+b^2+16 &=r^2 \label{eq:8}\\ a^2+12a+b^2+36 &=r^2 \label{eq:9} \end{align}\] Then subtracting the equations gives \[\begin{align*} \eqref{eq:9}-\eqref{eq:8}& \implies& -20a+20&=0&\implies& a=-1\\ \eqref{eq:8}-\eqref{eq:7}& \implies& 8b+8&=0 &\implies& b=-1. \end{align*}\]From equation \(\eqref{eq:7}\), we find that the radius of our circle is given by \[r^2=(-1)^2 + (-1)^2-8(-1)+16=26\] so the equation of the circle through \(A\), \(B\) and \(C\) is \[(x+1)^2+(y+1)^2=26.\]
Which method is quicker/easier here?
Again, probably the geometric method as the perpendicular bisectors weren’t algebraically fiddly to find.
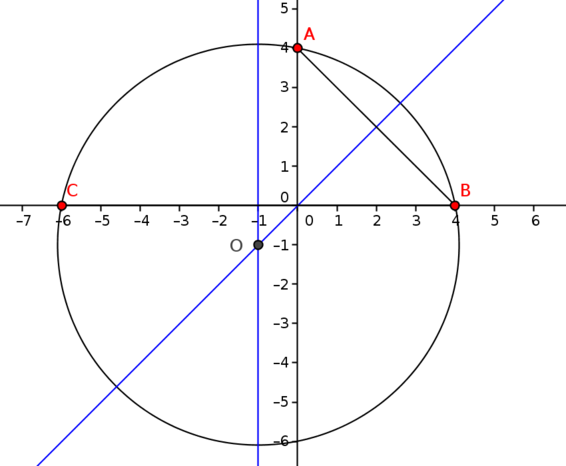
- \(A(-1,-5)\), \(B(-2,2)\), \(C(2,-1)\)
Geometric, perpendicular bisector method
The midpoint of \(AB\) is \(\left(-\dfrac{3}{2},-\dfrac{3}{2}\right)\) and the gradient of \(AB\) is \(\dfrac{-5-2}{-1-(-2)}=-7\). Thus the equation of the perpendicular bisector of \(AB\) is \[y-\left(-\frac{3}{2}\right)= \frac{1}{7}\left(x-\left(-\frac{3}{2}\right)\right)\] which we can rearrange to \[y=\frac{1}{7}x-\frac{9}{7}.\] Similarly, the midpoint of \(BC\) is \(\left(0,\dfrac{1}{2}\right)\) and its gradient is \(\dfrac{2-(-1)}{-2-2}=-\dfrac{3}{4}\). The equation of the second perpendicular bisector is therefore \[y-\frac{1}{2}=\frac{4}{3}x\] or \(y=\frac{4}{3}x+\frac{1}{2}\).
The two lines intersect when \[\frac{1}{7}x-\frac{9}{7}=\frac{4}{3}x+\frac{1}{2}\] which we can rearrange to get \[\begin{align*} &&\left(\frac{28}{21}-\frac{3}{21}\right)x&=-\frac{9}{7}-\frac{1}{2}&&\quad\\ \implies&& \frac{25}{21}x&=-\frac{25}{14}\\ \implies&& x&=-\frac{3}{2}. \end{align*}\]Substituting into the equation of the second perpendicular bisector (which has a simpler-looking equation), we find \[y=\frac{4}{3}\left(-\frac{3}{2}\right)+\frac{1}{2}=-\frac{3}{2}.\] Thus the centre of the circle is \(O\left(-\dfrac{3}{2},-\dfrac{3}{2}\right)\) and the radius is given by \[r^2=|OA|^2=\left(-1+\frac{3}{2}\right)^2+\left(-5+\frac{3}{2}\right)^2 =\frac{1}{4}+\frac{49}{4}=\frac{25}{2}.\] The final equation of the circle is therefore \[\left(x+\frac{3}{2}\right)^2+\left(y+\frac{3}{2}\right)^2=\frac{25}{2}.\]
Algebraic, simultaneous equations method
This time, our three simultaneous equations are: \[\begin{align} a^2+2a+b^2+10b+26&=r^2 \label{eq:10}\\ a^2+4a+b^2-4b+8&=r^2 \label{eq:11}\\ a^2-4a+b^2+2b+5&=r^2 \label{eq:12} \end{align}\] Then eliminating the squared terms, we find \[\begin{align} \eqref{eq:11}-\eqref{eq:10}& \implies& 2a-14b-18&=0&&\quad \label{eq:13}\\ \eqref{eq:12}-\eqref{eq:11}& \implies& -8a+6b-3&=0. \label{eq:14} \end{align}\]Eliminating \(a\): \[4\times\eqref{eq:13}+\eqref{eq:14} \implies -50b-75=0 \implies b=-\frac{3}{2}.\] Substitute this value for into equation \(\eqref{eq:14}\) to find \[-8a+6\times\left(-\frac{3}{2}\right)+3=0 \implies 8a=-12 \implies a=-\frac{3}{2}.\] (Alternatively, halving equation \(\eqref{eq:13}\) gives \(a-7b-9=0\), so \(a=7b+9=-\frac{3}{2}\).)
The radius is then given by \[r^2=\left(-1+\frac{3}{2}\right)^2+\left(-5+\frac{3}{2}\right)^2=\frac{1}{4}+\frac{49}{4}=\frac{25}{2}\] and the final equation of the circle is \[\left(x+\frac{3}{2}\right)^2+\left(y+\frac{3}{2}\right)^2=\frac{25}{2}.\]
Note that we can save ourselves a lot of effort by converting all fractions from mixed fractions like \(4\frac{1}{2}\) to \(\frac{9}{2}\) straightaway - this trick saves time when we are manipulating a lot of fractions.
Which method is quicker/easier here?
Tough call - which do you prefer?
It is interesting to notice that in the diagram for this part, the centre of the circle appears to lie on the chord \(AB\). Is this really the case?
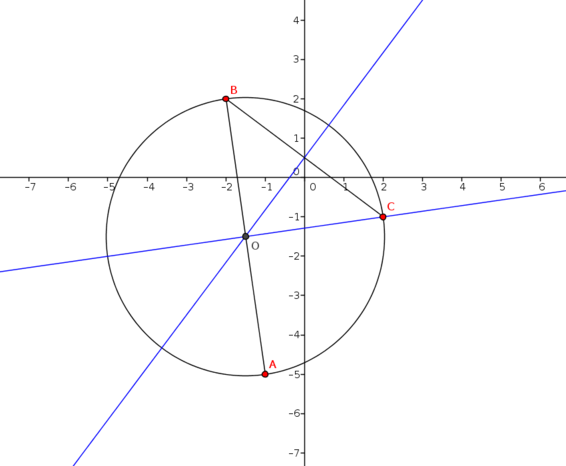
- \(A(3,3)\), \(B(1,-2)\), \(C(4,1)\)
Geometric, perpendicular bisector method
The midpoint of \(AB\) is \(\left(2,\dfrac{1}{2}\right)\) and the gradient of \(AB\) is \(\dfrac{3-(-2)}{3-1}=\dfrac{5}{2}\). Thus the equation of the first perpendicular bisector is \[y-\frac{1}{2}=-\frac{2}{5}(x-2)\] which can be rearranged to give \(y=-\frac{2}{5}x+\frac{13}{10}.\)
Likewise, the midpoint of \(BC\) is \(\left(\dfrac{5}{2},-\dfrac{1}{2}\right)\) and its gradient is \(\dfrac{-2-1}{1-4}=1\). The equation of the second perpendicular bisector is therefore \[y+\frac{1}{2}=-1\left(x-\frac{5}{2}\right)\] which gives \(y=2-x\).
The two lines intersect when \[\begin{align*} &&-\frac{2}{5}x+\frac{13}{10}&=2-x&&\quad\\ \implies&& \frac{3}{5}x&=\frac{7}{10}\\ \implies&& x&=\frac{7}{6}. \end{align*}\] Substituting into the equation of the second perpendicular bisector we find \[y=2-\frac{7}{6}=\frac{5}{6}.\] Thus the centre of the circle is \(O\left(\dfrac{7}{6},\dfrac{5}{6}\right)\) and the radius is given by \[\begin{align*} r^2=\vert OA \vert^2 &= \left(3-\frac{7}{6}\right)^2+\left(3-\frac{5}{6}\right)^2\\ &= \left(\frac{11}{6}\right)^2+\left(\frac{13}{6}\right)^2\\ &= \frac{121+169}{36}\\ &=\frac{145}{18}. \end{align*}\]The final equation of the circle is therefore \[\left(x-\frac{7}{6}\right)^2+\left(y-\frac{5}{6}\right)^2= \frac{145}{18}.\]
Algebraic, simultaneous equations method
Our three simultaneous equations are: \[\begin{align} a^2-6a+b^2-6b+18 &=r^2 \label{eq:15}\\ a^2-2a+b^2+4b+5 &=r^2 \label{eq:16}\\ a^2-8a+b^2-2b+17 &=r^2 \label{eq:17} \end{align}\] Eliminating the squared terms gives \[\begin{align} \eqref{eq:16}-\eqref{eq:15}& \implies& 4a+10b-13&=0&&\quad \label{eq:18}\\ \eqref{eq:17}-\eqref{eq:16}& \implies& -6a-6b+12&=0 \notag \\ \div (-6)& \implies& a+b-2&=0.\label{eq:19} \end{align}\] Eliminating \(a\): \[\eqref{eq:18}-4\times\eqref{eq:19} \implies 6b-5=0 \implies b=\frac{5}{6}.\] Substituting this value for \(b\) into equation \(\eqref{eq:19}\) gives \[a+\frac{5}{6}-2=0 \implies a=\frac{7}{6}.\] The radius is then given by \[\begin{align*} r^2&= \left(3-\frac{7}{6}\right)^2+\left(3-\frac{5}{6}\right)^2\\ &= \left(\frac{11}{6}\right)^2+\left(\frac{13}{6}\right)^2\\ &= \frac{121+169}{36}\\ &=\frac{145}{18} \end{align*}\]and thus the equation of the circle is \[\left(x-\frac{7}{6}\right)^2+\left(y-\frac{5}{6}\right)^2= \frac{145}{18}.\]
Which method is quicker/easier here?
Again, it’s a tough call - do you have a preference?