
Can you create an image like this using Desmos or other graphing software?
(Note: In Desmos, to draw the line \(y=2x\) only between \((0,0)\) and \((2,4)\), you would type “\(y=2x \{0<x<2\}\)” or “\(y=2x \{0<y<4\}\)”.)
The outer circle is centred on the origin so we can easily create this with an equation of the form \(x^2+y^2=r^2\). In the image \(r\) is not specified so we can take any value for our version. It might make sense to choose an integer so that the diagram is easier to read – let’s choose \(r=4\).
Now we have to find three straight lines that enclose an equilateral triangle. From the image we can assume that one vertex of our triangle must lie at coordinates \((4,0)\). We also know that because the circle is centred on the origin, the \(x\)-axis must be a line of symmetry of the equilateral triangle. Therefore we need the two straight lines that intersect to form this vertex to be inclined at \(\pm 30^\circ\) to the horizontal.
How do we find the gradients of these lines given the angles they make with the \(x\)-axis?
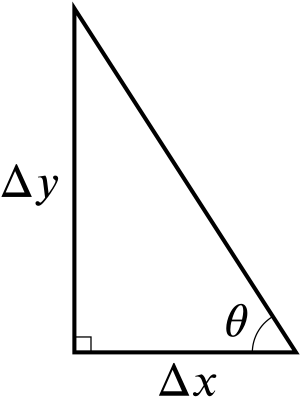
From the diagram above we see that a line that makes an angle \(\theta\) with the \(x\)-axis has gradient \(\frac{\Delta y}{\Delta x}=\tan{\theta}\) (up to sign). In our case \(\theta=30^\circ\), and we know that \(\tan{30^\circ}=\frac{1}{\sqrt{3}}\), so we know that the upward sloping line has gradient \(\frac{1}{\sqrt{3}}\) and the downward sloping line has gradient \(-\frac{1}{\sqrt{3}}\).
Now we have the gradients of the lines and a fixed point, \((4,0)\), on both we can use the general form of the equation of a straight line to give \[y-0=\pm \frac{1}{\sqrt{3}}(x-4),\] which can be simplified to \[\sqrt{3}y=x - 4 \qquad \textrm{and} \qquad \sqrt{3}y=-x+4.\]
To create an equilateral triangle we now need a third straight line to intersect the other two. Since the two lines we have just found are inclined at \(\pm 30^{\circ}\) to the horizontal, and we require the enclosed triangle to have all internal angles being \(60^{\circ}\), the third straight line must be vertical. It will therefore have an equation of the form \(x=a\) where \((a,0)\) is the other \(x\)-intercept of the triangle. The value of \(a\) can be found by looking at the right-angled triangle formed by the origin, the point \((a,0)\) and the vertex of the equilateral triangle at \((a,b)\) (which lies on the outer circle centred at the origin).
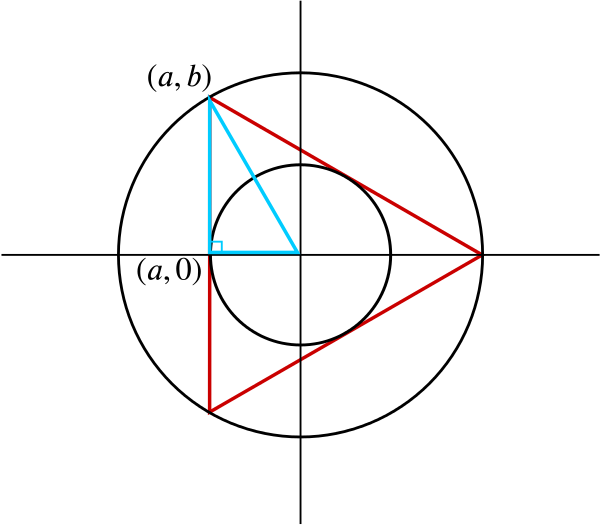
From the diagram we can see that the right-angled triangle in blue is one half of an equilateral triangle of side length \(4\). The vertical side bisects the base of this equilateral triangle and hence the base length of the blue right-angled triangle is \(2\).
Therefore the third straight line has the equation \(x=-2\).
It certainly appears that the inner circle is concentric with the outer circle (that is, it has the same centre). If this is the case, then the radius of the inner circle is clearly \(2\) and so the equation of the inner circle will be \(x^2+y^2=4\).
How can we show that the two circles are, indeed, concentric?
The inner circle touches the three sides of the triangle, so its centre is the point which is the same distance from all three sides. We’ll show that the origin has this property, so it must be the centre of the inner circle.
The origin is a distance of \(2\) from the vertical side, as we have just seen. From the following diagram, we see that the distance of the origin from the other sides is also \(2\), and so the origin is the centre of the inner circle.
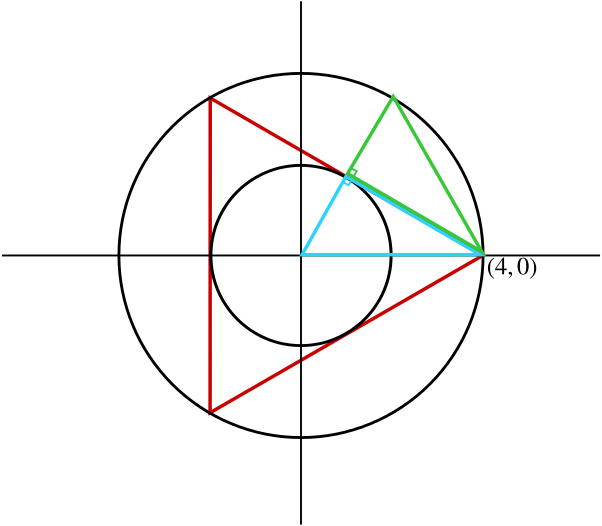
There is another way to think about this, using symmetry.
By symmetry we know that the centres of both circles lies on the \(x\)-axis, since if we reflect the picture along the \(x\)-axis, it must look the same. Likewise, if we reflect along the perpendicular bisector of one of the other sides of the triangle – which is also the angle bisector of the opposite angle, the shapes will also look the same. Therefore the centres of the two circles must coincide.
For each of the three outer circles given below, find the equation of the corresponding inner circle.
If we start with an outer circle of a different size, the construction will just be an enlargement of the example above. Therefore the inner circle will always have a radius half the size of the outer one.
\((x+2)^2+(y+1)^2=4\).
This is a circle of radius \(2\) with centre \((-2,-1)\). From above we can say that the radius of the corresponding inner circle will be \(1\) and the two circles are concentric. So the equation of the inner circle is \((x+2)^2+(y+1)^2=1\).
\((x-4)^2+y^2=9\)
This is a circle of radius \(3\) with its centre at \((4,0)\). From above we can say that the radius of the corresponding inner circle will be \(\frac{3}{2}\) and its centre at \((4,0)\). The equation of the inner circle is \((x-4)^2+y^2=\frac{9}{4}\).
\(x^2+y^2-3x-y=\frac{45}{2}\)
This circle is not in the same format as the previous two. Let’s start by completing the square to give \[\left(x-\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2+\left(y-\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2=\frac{45}{2}.\]
This simplifies to \[\left(x-\frac{3}{2}\right)^2+\left(y-\frac{1}{2}\right)^2-\frac{5}{2}=\frac{45}{2},\]
and then \[\left(x-\frac{3}{2}\right)^2+\left(y-\frac{1}{2}\right)^2=\frac{50}{2}=25.\]
Now we can see that this represents a circle of radius \(5\) and centre \((\frac{3}{2},\frac{1}{2})\). So, applying the same reasoning as in the previous two problems we have that the inner circle has a radius of \(\frac{5}{2}\) and centre \((\frac{3}{2},\frac{1}{2})\).
Therefore the equation of the corresponding inner circle is \[\left(x-\frac{3}{2}\right)^2+\left(y-\frac{1}{2}\right)^2=\frac{25}{4}.\]
For each of the three inner circles given below, find the equation of the corresponding outer circle.
We will now apply our reasoning from the problems above in reverse.
\(\left(x-3\right)^2+\left(y+\frac{1}{2}\right)^2=16\)
This equation represents a circle of radius \(4\) and centre \((3,-\frac{1}{2})\). From our previous work we know that the radius of the outer circle is double that of the inner circle and that the two circles are concentric. Therefore we have that the outer circle has a radius of \(8\) and centre \((3,-\frac{1}{2})\).
The equation of the outer circle will then be \((x-3)^2+(y+\frac{1}{2})^2=64\).
\(\left(x+\frac{3}{2}\right)^2+\left(y-\frac{3}{2}\right)^2=8\)
This represents a circle of radius \(\sqrt{8}\) and centre \((-\frac{3}{2},\frac{3}{2})\). The corresponding outer circle will therefore have a radius of \(2\sqrt{8}\) and the same centre. Its equation will therefore be \((x+\frac{3}{2})^2+(y-\frac{3}{2})^2=32\).
\(x^2+y^2+14y+29=0\)
If we adopt the same approach as for question 3 above then by completing the square we get \[x^2+\left(y+7\right)^2-7^2+29=0.\] Simplifying then gives \[x^2+(y+7)^2=20,\] from which we can see that we have a circle of radius \(\sqrt{20}\) and centre \((0,-7)\). The equation of the outer circle will now be \(x^2+(y+7)^2=80\).
Find the area of the equilateral triangle in terms of \(r\), the radius of the inner circle.
Look at the diagram below.
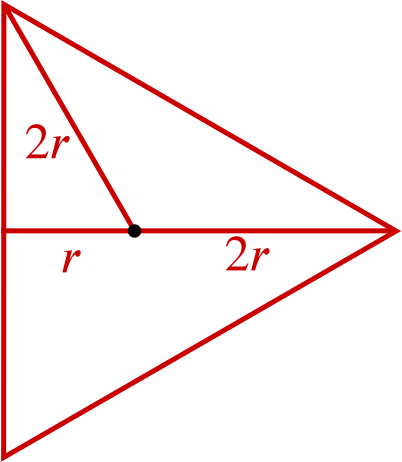
Using Pythagoras’ Theorem we have that one half of the side length of the equilateral triangle is \(\sqrt{(2r)^2-r^2}=\sqrt{3}r\).
Then the area of the equilateral triangle will be given by \(3r \times \sqrt{3}r=3\sqrt{3}r^2\).

Can you create an image like this using Desmos?
This image is the same as the first but with a second equilateral triangle. This second triangle is the first reflected in the \(y\)–axis.
It is fairly clear from the diagram that the vertical straight line on the right will be given by the equation \(x=2\). Then the other two straight lines will have gradients of \(\pm \frac{1}{\sqrt{3}}\) as before, this time intersecting at \((-4,0)\). Using the general form of the equation of a straight line we get \[y-0=\pm\frac{1}{\sqrt{3}}(x+4),\] which simplifies to \[\sqrt{3}y=x+4 \qquad \textrm{and} \qquad \sqrt{3}y=-x-4.\]
Show that the ratio of the area of the original equilateral triangle to that of the enclosed hexagon is \(3:2\).
The enclosed hexagon can be divided into six smaller equilateral triangles, each of height \(r\) (where \(r\) is the radius of the inner circle). The original triangle consists of those six smaller equilateral triangles plus another three. So the ratio of the area of the original equilateral triangle to that of the enclosed hexagon is \(9:6\) or \(3:2\) as required.

