Show that the equation of any circle passing through the points of intersection of the ellipse \[(x + 2)^2 + 2y^2 = 18\] and the ellipse \[9(x - 1)^2 + 16y^2 = 25\] can be written in the form \[x^2 - 2ax + y^2 = 5 - 4a.\]
To get some sense of what is going on in this question, it is helpful to sketch a graph.
Both ellipses are symmetrical in the \(x\)-axis, since replacing \(y\) with \(-y\) makes no difference to the equations.
The second ellipse is symmetrical in the line \(x=1\), since if we substitute in \(x=1+k\) and \(x=1-k\) into the equation, we obtain the same values for \(y\). Likewise, the first ellipse is symmetrical in \(x = -2\). (For more on this idea, have a look at Quadratic symmetry.)
If we put \(x = 0\), and then \(y = 0\) into each equation, we can find the intercepts with the axes.
Alternatively, we could observe that the centre of the first ellipse lies at \((-2,0)\) and its semi-axes have length \(\sqrt{18}=3\sqrt{2}\) in the \(x\)-direction and \(\sqrt{9}=3\) in the \(y\)-direction. Likewise, the second ellipse has centre \((1,0)\) and semi-axes \(\frac53\) and \(\frac54\).
Either of these approaches gives us enough information to sketch the ellipses.
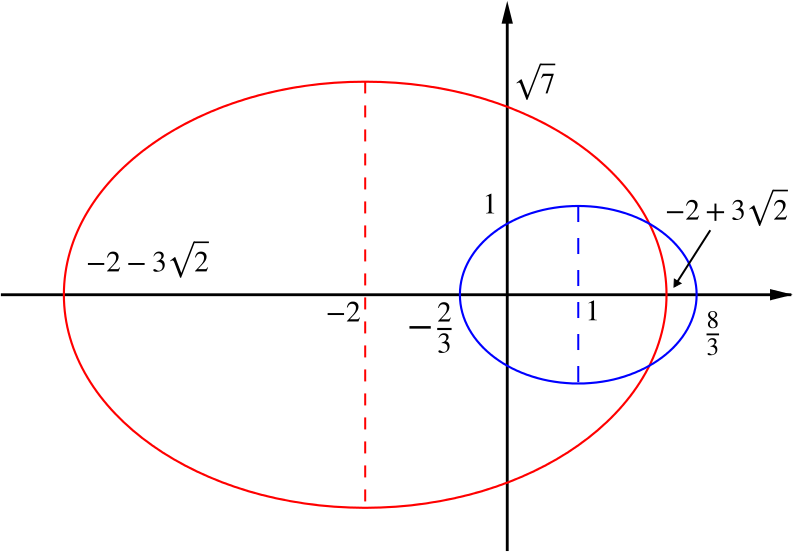
(Though it is not obvious without a calculator whether \(-2+3\sqrt{2}<\frac83\) or not, the question does tell us that the ellipses intersect. Our calculation of their point of intersection will then prove that they do, indeed, intersect, and it will follow that \(-2+3\sqrt{2}<\frac83\).)
We can now tackle the question asked.
We find the points of intersection of the two ellipses by solving the simultaneous equations \[(x + 2)^2 + 2y^2 = 18\] and \[9(x - 1)^2 + 16y^2 = 25.\]
We can eliminate \(y\) by multiplying the first equation by \(8\) and subtracting the second equation, giving \[\begin{align*} && 8(x + 2)^2 - 9(x - 1)^2 &= 144 - 25&&\quad\\ \iff\quad && 8x^2 + 32x + 32 - 9x^2 + 18x - 9 &= 119\\ \iff\quad && x^2 - 50x + 96 &= 0\\ \iff\quad && (x - 2)(x - 48) &= 0. \end{align*}\]This gives the \(x\)-value of the points of intersection as either \(2\) or \(48\).
It is clear from our sketch that \(x=48\) does not correspond to real points of intersection. (There are, though, complex points of intersection.) So we must have \(x=2\). (We could also find this by substituting \(x=48\) into the equation of the ellipse and discovering that there are no real values of \(y\) corresponding to it.)
Taking \(x = 2\) and substituting into the first simultaneous equation, we have \[\begin{align*} && 16 + 2y^2 &= 18&&\quad\\ \iff\quad&& y^2 &= 1\\ \iff\quad&& y &= \pm1. \end{align*}\]Hence there are two (real) points of intersection, at \((2,1)\) and \((2,-1)\). (It’s easy to check that these points really do lie on both ellipses).
A circle through both these points has centre \((a,0)\) on the \(x\)-axis, by symmetry.
Then the equation of the circle is \[(x - a)^2 + y^2 = (2-a)^2+1.\] The right-hand side here is the distance of the centre from \((2,1)\), or from \((2,-1)\), squared.
Expanding gives \[\begin{align*} && x^2 - 2ax + a^2 + y^2 &= 5 - 4a + a^2&&\quad\\ \iff\quad&& x^2 - 2ax + y^2 &= 5 - 4a, \end{align*}\]as required.
These circles form a system of coaxal circles; you might like to explore this concept further.

