When does this area within a circle have a maximum value?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

If two chords \(PQ\) and \(PR\) on a circle of radius \(1\) meet in an angle \(\theta\) at \(P\), for example as drawn in the diagram below,

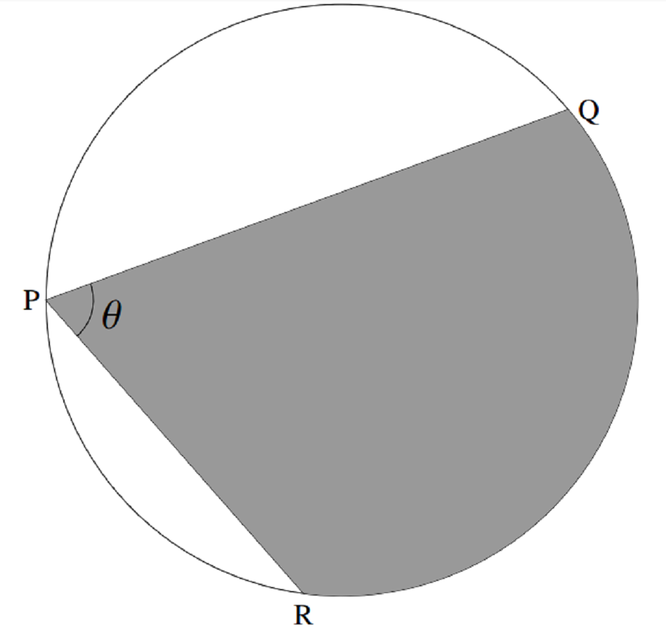
then the largest possible area of the shaded region \(RPQ\) is

1. \(\theta(1 + \cos\dfrac{\theta}{2})\); \(\quad\)\(\quad\)(b) \(\theta + \sin\theta\); \(\quad\)\(\quad\)(c) \(\dfrac{\pi}{2}(1-\cos\theta)\);\(\quad\)\(\quad\) (d) \(\theta\).