If two chords \(PQ\) and \(PR\) on a circle of radius \(1\) meet in an angle \(\theta\) at \(P\), for example as drawn in the diagram below,
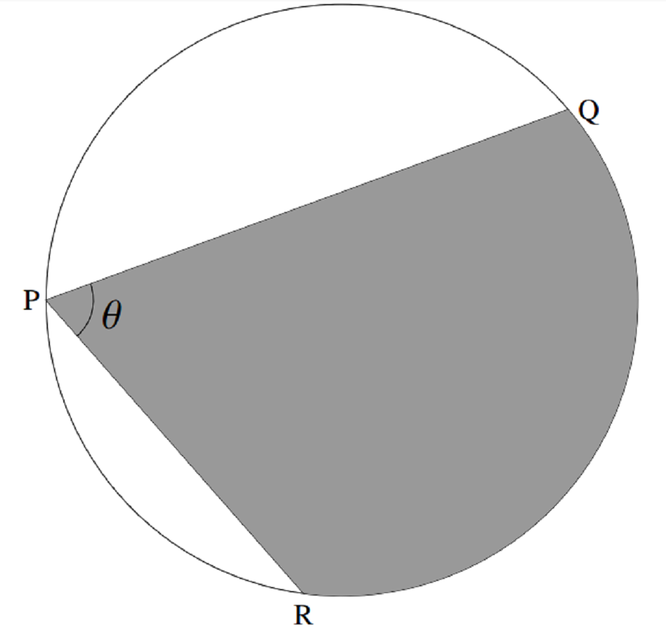
then the largest possible area of the shaded region \(RPQ\) is
- \(\theta(1 + \cos\dfrac{\theta}{2})\); \(\quad\)\(\quad\)(b) \(\theta + \sin\theta\); \(\quad\)\(\quad\)(c) \(\dfrac{\pi}{2}(1-\cos\theta)\);\(\quad\)\(\quad\) (d) \(\theta\).
Can we say anything about how the chords must be aligned to make the shaded area a maximum for a given \(\theta\)?
Can we draw the diagram for this maximal situation and, marking in the angles we know, calculate the required area?

