If two chords \(PQ\) and \(PR\) on a circle of radius \(1\) meet in an angle \(\theta\) at \(P\), for example as drawn in the diagram below,
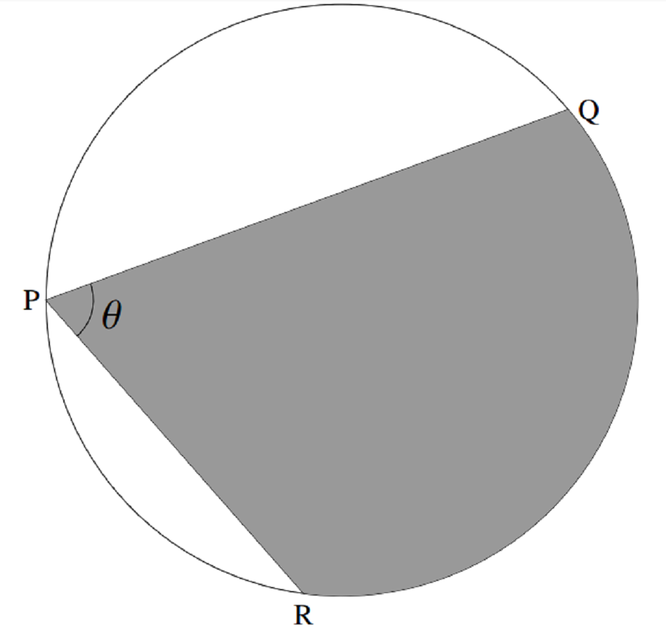
then the largest possible area of the shaded region \(RPQ\) is
- \(\theta(1 + \cos\dfrac{\theta}{2})\); \(\quad\)\(\quad\)(b) \(\theta + \sin\theta\); \(\quad\)\(\quad\)(c) \(\dfrac{\pi}{2}(1-\cos\theta)\);\(\quad\)\(\quad\) (d) \(\theta\).
The shaded area will be a maximum when the diagram is symmetrical.
We can see this as follows; imagine rotating \(PR\) through a small angle \(\alpha\) anticlockwise in the diagram above.
To keep \(\theta\) the same size we need to rotate \(PQ\) through \(\alpha\) also, and since \(PQ\) is longer than \(PR\), this will cut off a greater area than rotating \(PR\) did.
Thus the symmetrical arrangement maximises the shaded area.
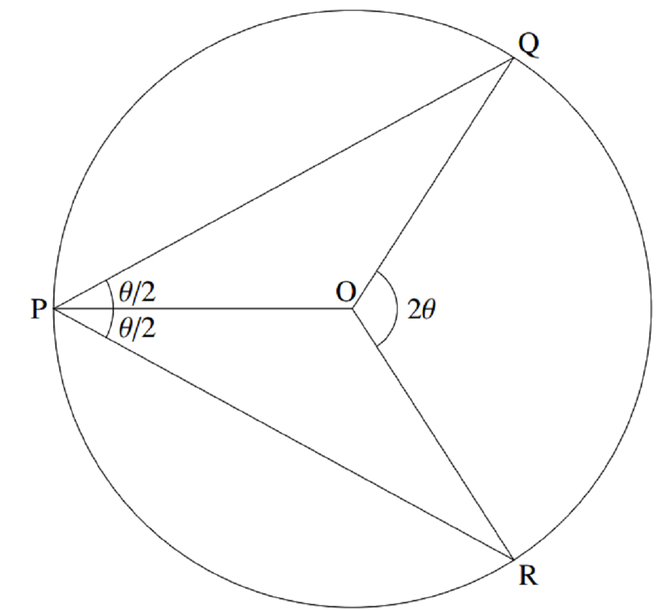
So we need to find the shaded area for the situation above.
Remember that the area of a sector enclosing an angle \(\theta\) (in radians) and with radius \(r\) is \(\dfrac{1}{2}r^2 \theta\).
The area of the sector we need is \(\dfrac{1}{2}\times 1^2 \times 2\theta = \theta.\)
Remember that the area of a triangle with sides \(a\) and \(b\) enclosing an angle \(C\) is \(\dfrac{1}{2}ab\sin C\).
The sum of the areas of the two triangles \(POR\) and \(POQ\) is \(2\left[\dfrac{1}{2}\times 1^2 \times \sin (\pi - \theta)\right] = \sin (\pi - \theta)] = \sin \theta.\)
Thus the total shaded area is \(\sin \theta + \theta\), and the answer is (b).

