A variable point \(P\) on the circle \(x^2+y^2=a^2\) has coordinates \((a\cos\theta,a\sin\theta)\), and \(A\) is the fixed point \((c,0)\).
If \(Q\) is the point on \(AP\) such that \(AQ:QP=\lambda:1\), find the coordinates of \(Q\), and show that the locus of \(Q\) is another circle. Calculate the coordinates of the centre of this circle and the length of its radius.
Approach 1
We begin by sketching the circle of radius \(a\) about the origin, the point \(P\) and the point \(A\). We will consider the line \(AP\) and a point \(Q\) such that \(AQ=\lambda QP\).

Here we have drawn the diagram in the case where \(c>a\). Would our answer be any different if we had \(0<c<a\) or \(c<0\)?
Let the co-ordinates of \(Q\) be \((x,y)\) and consider the lengths we know in the following diagram. As we are given co-ordinates, we will add horizontal and vertical lines from \(Q\).

By corresponding angles, the triangles with hypotenuses \(AQ\) and \(QP\) have the same three angles and so are similar. Hence the ratios of the opposite sides, adjacent sides and hypotenuses are equal and so
\[\frac{c-x}{x-a\cos\theta} = \frac{y}{a\sin\theta-y} =\frac{\lambda}{1}.\]
This rearranges to give
\[c-x = \lambda x - \lambda a\cos\theta \qquad \text{and} \qquad y = \lambda a\sin\theta - \lambda y\]
and hence
\[Q=(x,y)=\left(\frac{\lambda a\cos\theta + c}{\lambda+1},\frac{\lambda a\sin\theta}{\lambda+1}\right).\]
We want to show that this sweeps out a circle as \(\theta\) varies from \(0\) to \(2\pi\).
We currently have equations for \(x\) and \(y\) in terms of \(\theta\) and so, to show that this is a circle, we can start by trying to eliminate \(\theta\) and expressing the locus in terms of just \(x\) and \(y\).
The easiest way to do this is to use the identity \(\cos^2 \theta +\sin^2 \theta = 1\). Rearranging our expressions for \(x\) and \(y\) gives that
\[\cos\theta = \left(\frac{\lambda+1}{\lambda a}\right) \left(x - \frac{c}{\lambda+1}\right) \qquad \text{and} \qquad \sin\theta = \left(\frac{\lambda+1}{\lambda a}\right) y.\]
Substituting this in to our identity and dividing through by the common factor gives
\[\left(x - \frac{c}{\lambda+1}\right)^2 + y^2 = \left(\frac{\lambda a}{\lambda+1}\right)^2\]
and so the locus of \(Q\) is a circle with centre \(\left(\dfrac{c}{\lambda+1},0\right)\) and radius \(\dfrac{\lambda a}{\lambda+1}\).
Approach 2
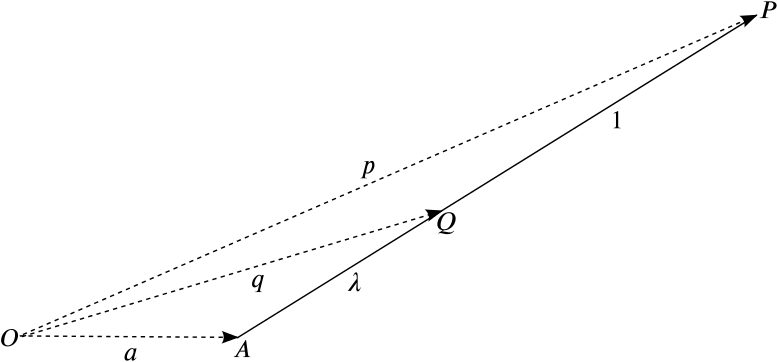
Consider the stripped down diagram of the problem.
We let the point \(P\) have position vector \(\mathbf{p}=(a\cos\theta,a\sin\theta)\), \(A\) the vector \(\mathbf{a}=(c,0)\) and the (currently unknown) point \(Q\) the vector \(\mathbf{q}\).
Travelling along the vector from \(A\) to \(P\) we follow the vector equation \[\mathbf{r} = \mathbf{a} + \mu(\mathbf{p} - \mathbf{a}) = \left(\begin{array}{c} c \\ 0 \end{array}\right) + \mu \left(\begin{array}{c} a\cos\theta - c \\ a\sin\theta \end{array}\right),\] where \(0\leq \mu \leq 1\).
It’s given that \(AQ:QP=\lambda:1\), so point \(Q\) is \(\frac{\lambda}{\lambda+1}\) along the line from point \(A\).
Therefore, if we let \(\mu=\frac{\lambda}{\lambda+1}\) we will be at point \(Q\) so we can then find its coordinates: \[\mathbf{q}=\left(\begin{array}{c} c \\0 \end{array}\right)+\frac{\lambda}{\lambda+1}\left(\begin{array}{c} a\cos\theta - c \\ a\sin\theta \end{array}\right),\] so, using the same definition of \(x\) and \(y\) from before we again find that \[\begin{align*} x &= c+ \frac{\lambda}{\lambda+1}a\cos\theta - \frac{\lambda c}{\lambda+1}= \frac{c}{\lambda+1} + \frac{\lambda}{\lambda+1}a\cos\theta, \\ y &= \frac{\lambda}{\lambda+1}a\sin\theta \end{align*}\]so again \[\left(x-\frac{c}{\lambda+1}\right)^2+y^2=\frac{\lambda^2a^2}{(\lambda+1)^2},\]
which leads to the same conclusion.
Show that the condition for the two circles to intersect at right angles is \(\,c^2=a^2(1+2\lambda+2\lambda^2)\).
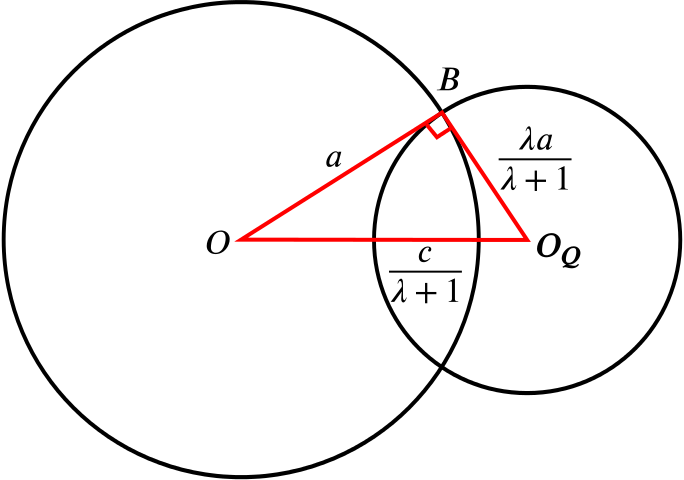
The two circles intersect at right angles if and only if there is a right-angled triangle formed by the points \(O(0,0)\), \(O_Q\left(\dfrac{c}{\lambda+1},0\right)\) and one of the intersection points, which we will have labelled \(B\).
The triangle \(OBO_Q\) is a right-angled triangle if and only if the lengths of the sides obey Pythagoras’s theorem: \[a^2+\frac{\lambda^2 a^2}{(\lambda+1)^2}=\frac{c^2}{(\lambda+1)^2}\] \[\iff \quad c^2=a^2(1+2\lambda+2\lambda^2)\] as required.

