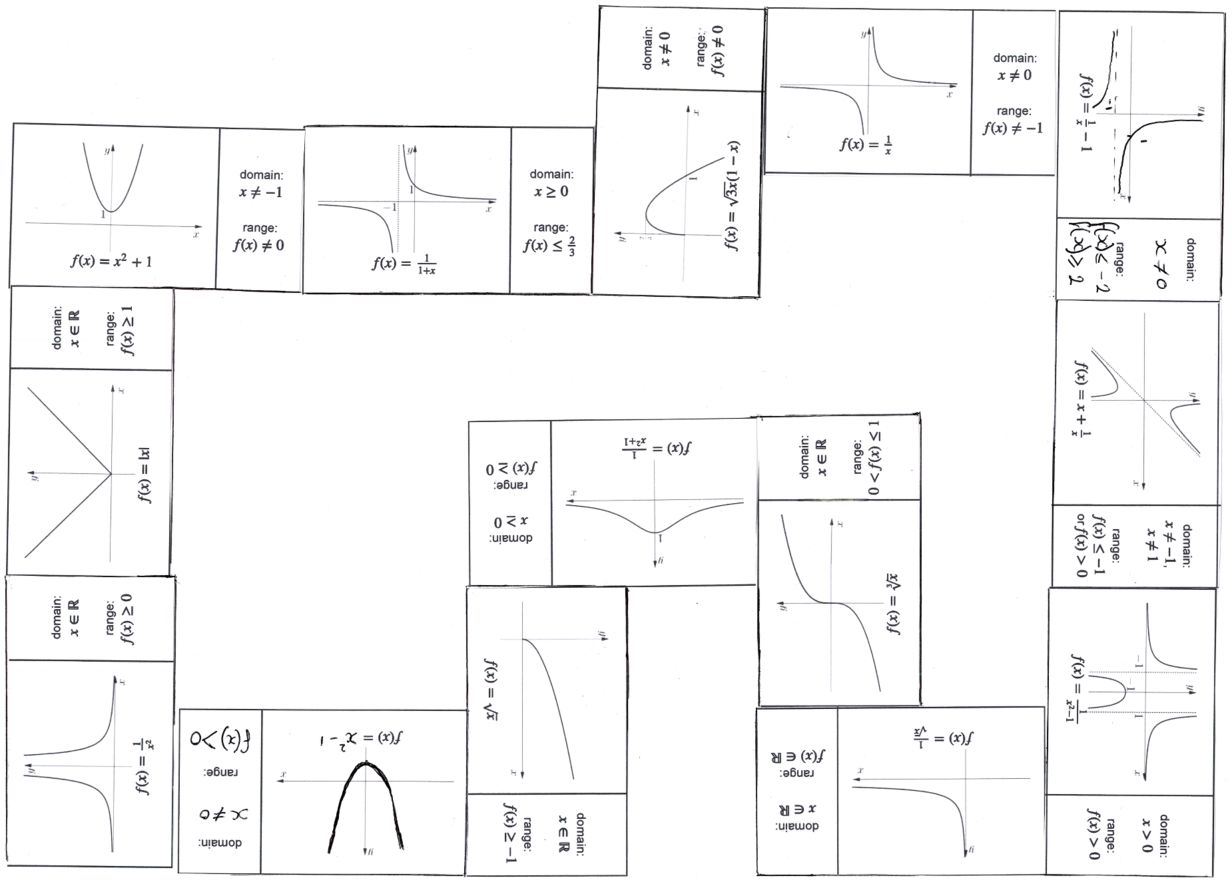
Unrestricted domains
In this exercise we are using domain to mean all the possible values of \(x\). In other contexts, we may artificially restrict the domain of a function. For instance we might only be interested in the function \(f(x)=x^2\) in the domain \(0\le x<2\).
Similar inequalities
With some of the functions you have to be careful to distinguish between, for instance, \(x>0\) and \(x\ge0\).
Multiple inequalities
One of the functions has a range that is between \(0\) and \(1\), including \(1\) but not including \(0\). This can be written neatly as \(0<f(x)\le1\).
Another has a range that includes all numbers \(>0\) and all numbers \(\le-1\) but not numbers in between. This has to be written as two separate inequalities.
Turning points of \(x+\frac{1}{x}\)
Finding the range of \(f(x)=x+\frac{1}{x}\) depends on knowing the value of the function at its turning points (maximum and minimum) and this is not given on the card. There is more than one way to find these values; here are a few.
Using calculus
We could differentiate the function and thus find when its gradient is zero.
Using an inequality
By substitution we can find that \(f(1)=2\). Is there any positive \(x\) value for which \(f(x)<2\)? If so, \[\begin{align*} x+\frac{1}{x}&<2\\ x^2+1&<2x \text{ .} \end{align*}\]Rearranging and factorising leads to an inequality with no real solutions, so \(2\) must be the minimum value of \(f(x)\) for positive \(x\). The local maximum can be found by symmetry.
When rearranging the inequality, why does it matter that the question specified positive \(x\) values?
By adding gradients
Notice that \(f(x)\) is the sum of two functions: \(x\) and \(\frac{1}{x}\). So the gradient of \(f(x)\) is the sum of the gradients of \(x\) and \(\frac{1}{x}\) (it is possible to prove this, but we aren’t going to do so here!).
\(y=x\) has gradient \(1\), so the turning points of \(f(x)\) will be where \(y=\frac{1}{x}\) has gradient \(-1\). Can you find the \(x\) values where this happens?