Sketch the graph of \(y=\dfrac{1}{x+a}\) for different values of \(a\). We suggest you start by trying the values \(a=0\), \(1\), \(-1\).
What do you notice?
Can you explain your observations?
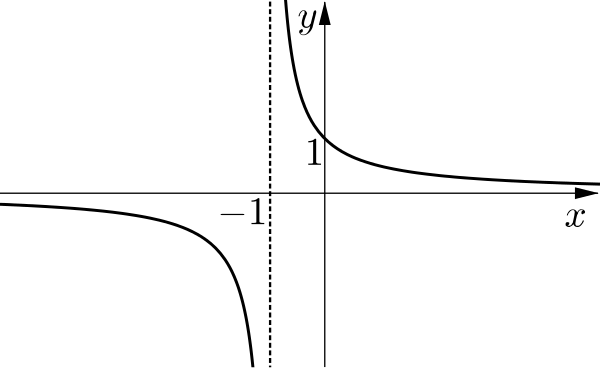
The graph of \(y=\dfrac{1}{x}\) is familiar. The family of graphs of \(y=\dfrac{1}{x+a}\) all look very similar.
Can you describe how they are related and the significance of the value \(a\)?
Now sketch the graph of \(y=\dfrac{1}{x^2+a}\) for different values of \(a\), again starting with \(a=0\), \(1\), \(-1\).
What do you notice this time?
Can you explain why the graphs behave in this way?
The shape of these graphs is very different for different values of \(a\). We can split our graphs into the cases \(a<0\), \(a=0\) and \(a>0\).
When \(a=0\)
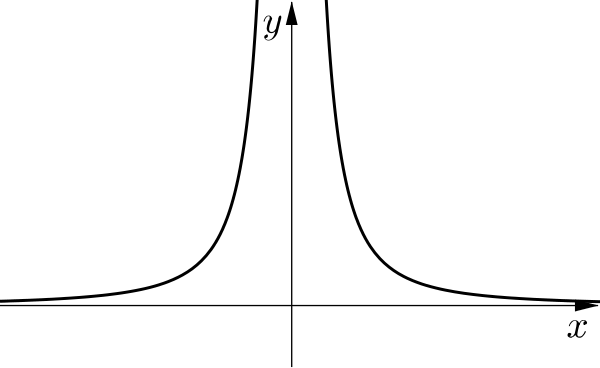
This is the familiar graph \(y=\dfrac{1}{x^2}\).
We can visualise it as the reciprocal of \(y=x^2\).
- When \(x=0\), \(x^2=0\) so \(y=\frac{1}{x^2}\) has a vertical asymptote.
- As \(x\) increases, \(x^2\) increases so \(\frac{1}{x^2}\) decreases towards zero.
- The function is even since the \(x\) value is squared, so the \(y\)-axis is a line of symmetry.
When \(a<0\)
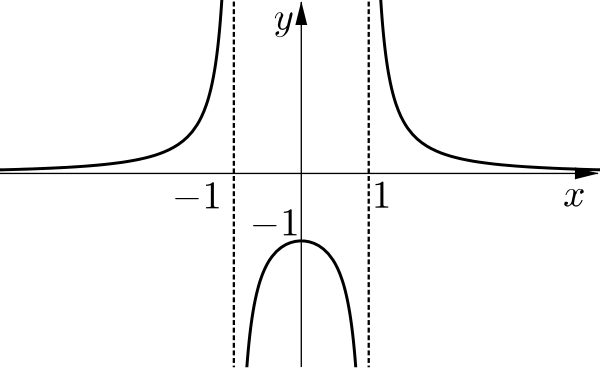
We might have expected \(y=\dfrac{1}{x^2-1}\) to be a translation of \(y=\dfrac{1}{x^2}\), but instead it does something much more interesting!
To understand this behaviour, we could think about the graph of \(y=x^2-1\) and what the reciprocal will look like, paying particular attention to where it crosses the \(x\)-axis. How, then, does the shape of \(y=\dfrac{1}{x^2+a}\) change as \(a\) takes negative values other than \(-1\)?
Another way to visualise this is to rewrite the function in terms of other functions whose graphs we are familiar with. Since \(a\) is negative, we could rewrite our function as \(y=\dfrac{1}{x^2-b^2}\) (where \(b^2=-a\)). Can you now rewrite this further?
When \(a>0\)
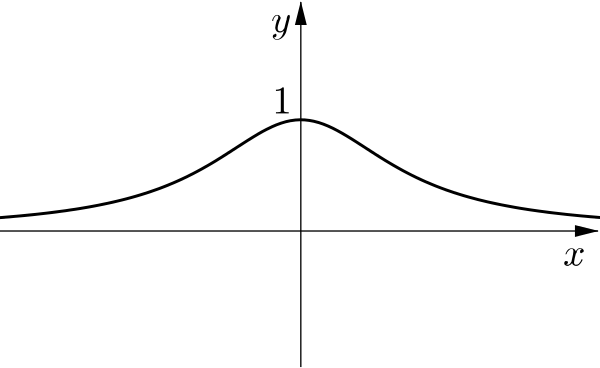
Now, we find that there are no vertical asymptotes. Can you explain why by thinking about the graph of the quadratic \(y=x^2+1\)?
What if we rewrite this function as \(y=\dfrac{1}{x^2+b^2}\)? Can you expand this as we did above?
In this case, when \(a>0\), what happens to the graph as \(a\) takes different positive values?
Joining them up
As \(a\) gets close to zero, can you visualise how each of these more interesting graphs will become closer and closer to the graph of \(y=\dfrac{1}{x^2}\)?
Use graphing software or the applets in the next section to view this transition.

