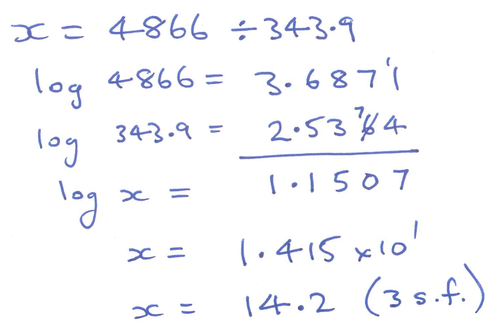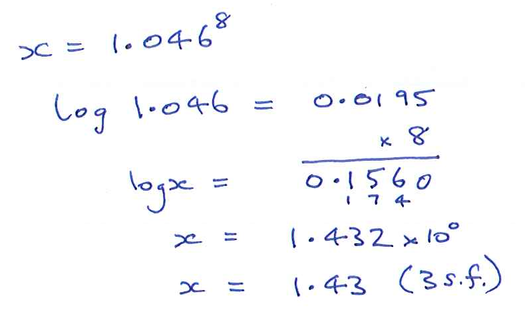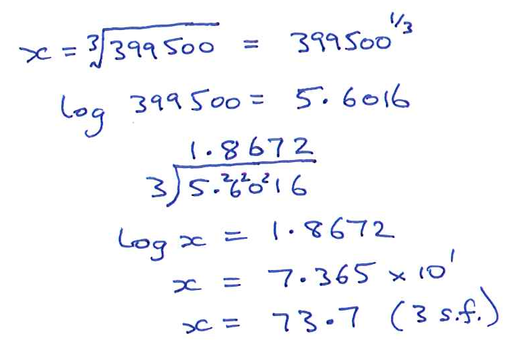1950s calculators

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

In the previous section we used log tables to find the logarithms of numbers given to three significant figures. You may have noticed that the tables have extra columns at the right. These are called “difference columns” and allow us to look up the logarithms of numbers given to four significant figures.

The following video shows someone calculating \(28{\cdot}27{\times}185{\cdot}7\).

Practise using the log tables to calculate \[173{\cdot}5{\times}6{\cdot}384\] and check your answer using an electronic calculator.

Can you apply the other laws of logarithms to calculate the following using log tables?

1. \(\dfrac{4866}{343{\cdot}9}\)

2. \(1{\cdot}046^8\)

3. \(\sqrt[3]{399500}\)

You can check your working and your solutions here.

Solution 1

\(\dfrac{4866}{343{\cdot}9}\)

Solution 2

\(1{\cdot}046^8\)

Solution 3

\(\sqrt[3]{399500}\)