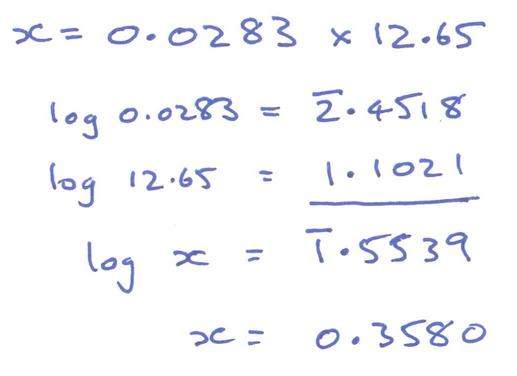Now here is the full version of the 1952 exam question we started with earlier.
Use logarithms to calculate, correct to three significant figures, \[\frac{1{\cdot}152\times(3{\cdot}902)^3}{(5{\cdot}463)^2} .\]
The area of a square field is \(5{\cdot}355\) hectares. Find, correct to the nearest metre, the length of a diagonal of the field.
[1 hectare = 100 ares; 1 are = 1 square dekametre.]
[Editorial note: 1 dekametre = 10 metres.]
UCLES O level Elementary Mathematics Alternative A: Arithmetic, Question 7, 14 July 1952 (slightly amended)
One final twist
In this resource we have dealt only with the logarithms of numbers greater than \(1\). Can you see the difficulty with using log tables to do calculations with numbers such as \(0{\cdot}0283\) ?