Can you arrange some of these logarithms to complete the grid below? The values of the logarithms need to increase along the rows and down the columns. Try to do this without using a calculator.
\[ \log_{3} 2 \quad \log_{4} 5 \quad \log_{2} 5 \quad \log_{3} 4 \quad \log_{3} 5 \quad \log_{5} 3 \] \[ \log_{2} 3 \quad \log_{5} 2 \quad \log_{5} 4 \quad \log_{4} 3 \quad \log_{4} 2 \quad \log_{2} 4 \]
| Increasing size \(\longrightarrow\) | |||
|
Increasing size \(\downarrow\) |
\(\log_{\square} \square\) | \(\log_{\square} \square\) | \(\log_{\square} \square\) |
| \(\log_{\square} \square\) | \(1\) | \(\log_{\square} \square\) | |
| \(\log_{\square} \square\) | \(\log_{\square} \square\) | \(\log_{\square} \square\) | |
If we think about putting some of these logarithms in order, perhaps by visualising the graph of a logarithmic function or remembering that \(\log_2 x\) is an increasing function, we can form inequalities such as \[\log_{2} 3 < \log_{2} 4 < \log_{2} 5\] and \[\log_{3} 2 < \log_{3} 4 < \log_{3} 5 .\]
Next, we can form inequalities such as \[\log_{5} 3 < \log_{4} 3 < \log_{2} 3\] either by
- thinking about what the base of a logarithm means (we require a smaller power of \(5\) than of \(4\) to make \(3\)), or by
- changing the base (\(\log_{4} 3=\log_{4} 5\times\log_{5} 3\) and \(\log_{4} 5>1\)), or by
- noting that \(\log_x 3\) is a decreasing function.
Finally, there are a number of ways to obtain an inequality such as \[\log_{5} 2 < 1 < \log_{2} 5 .\] For instance,
- remember that \(\log_{2} 5\) is the power to which we need to raise \(2\) in order to get \(5\), so it must be greater than \(1\). Similarly, \(\log_{5} 2\) must be less than \(1\). Or,
- write \(1\) as \(\log_{5} 5\) and use the ideas above to obtain the inequality \(\log_{5} 2 < \log_{5} 5 =1\). Similarly, \(\log_2 5>\log_{2} 2=1\). Or,
- use the rule for changing the base: \(\log_{5} 2\times\log_{2} 5=\log_{5} 5=1\) so the two logarithms are reciprocals.
We have referred to a lot of different ideas here. Make sure you can convince yourself that the reasoning is all correct.
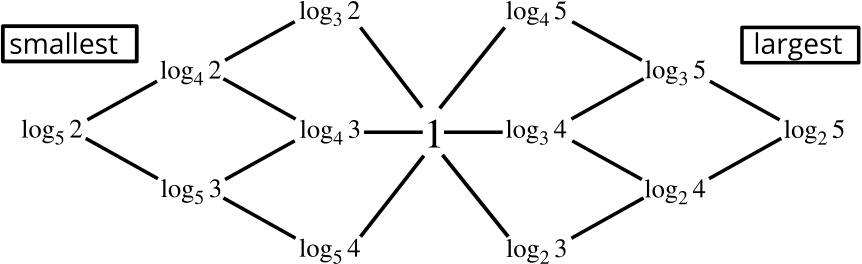
Using all these ideas, can you summarise what we know about the order of the logarithms in some kind of a diagram?
For the second grid, our network of inequalities doesn’t give quite enough information to complete the bottom-left and top-right cells. However, we know that \(\log_{2}4 = 2\), and if we let \(\log_{3} 5=x\) then \(3^{x}=5\), so \(x\) must be less than \(2\). Therefore \[\log_{3} 5 < \log_{2}4 .\]
We can use a similar argument starting with \(\log_{4}2\) to give us a solution. Or we could think about reciprocals: \[\log_{5} 3=\frac{1}{\log_{3} 5} \quad\text{ and }\quad \log_{4}2=\frac{1}{\log_{2}4}\] and use that to write another inequality based on the one above.
See the resource Changing bases for an exploration of the rule for changing bases and the behaviour of logarithmic functions.