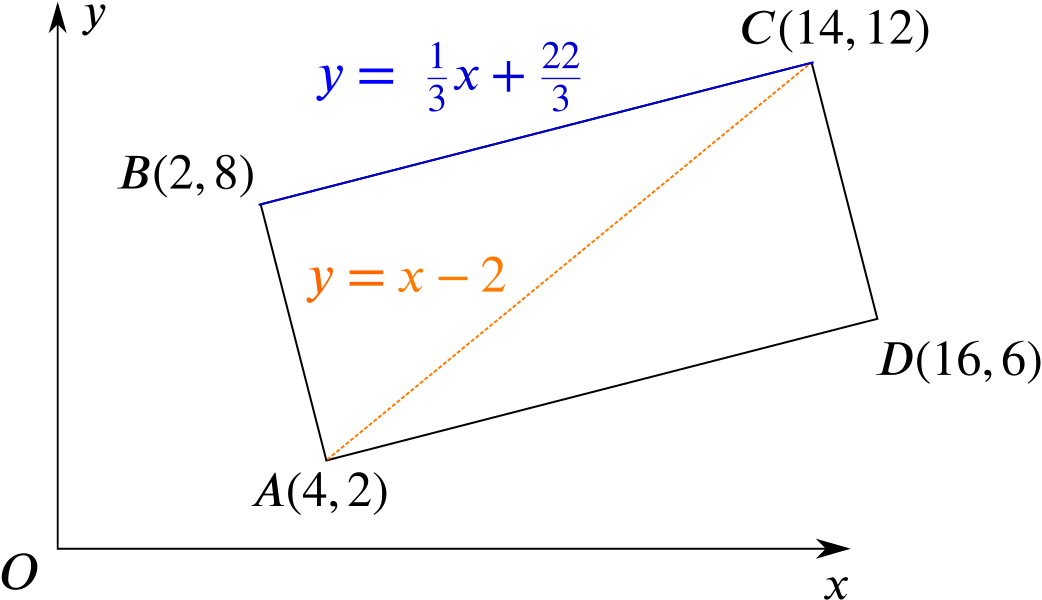Can we find the coordinates of this tilted rectangle?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

The gradient of \(AB\) is \(\dfrac{8-2}{2-4} = - 3\). The gradient of the perpendicular line \(BC\) is thus \(\dfrac {1}{3}\).

Since we know that the line passes through \(B(2,8)\), the equation of \(BC\) is given by \[y-8 = \frac{1}{3}(x-2)\] which we can rearrange as \(y = \dfrac{1}{3}x+\dfrac{22}{3}\) or \(3y=x+22\).

We know that \(BC\) and \(AC\) meet at \(C\). We can calculate their intersection point by setting their equations equal to each other (solving their equations simultaneously). We then have \[\begin{align*} &&x-2&= \frac{1}{3}x+\frac{22}{3}&&\quad\\ \iff\quad&& \frac{2}{3}x&=\frac{28}{3}\\ \iff\quad&& x&=14. \end{align*}\]

The corresponding \(y\) value is then \(y=14-2=12\), so \(C\) has coordinates \((14,12)\).

Going from \(B\) to \(C\) is the same translation as going from \(A\) to \(D\). (In terms of vectors, \(\overrightarrow{BC}=\overrightarrow{AD}\).) To get from \(B (2,8)\) to \(C (14,12)\), we move \(12\) units to the right and \(4\) units up.

So if we start at \(A (4,2)\) and move \(12\) units to the right and \(4\) units up, we arrive at \(D(16,6)\).

The length of the side \(AB\) can be calculated using Pythagoras’ theorem, giving \[\begin{align*} AB &= \sqrt{(x_A-x_B)^2+(y_A-y_B)^2}\\ &= \sqrt{(2)^2+(-6)^2}\\ &= \sqrt{40}\\ &= 2\sqrt{10}. \end{align*}\] In the same way we can find \(BC\): \[\begin{align*} BC &= \sqrt{(x_B-x_C)^2+(y_B-y_C)^2} \\ &= \sqrt{(-12)^2+(-4)^2} \\ &=\sqrt{160}\\ &= 4\sqrt{10}. \end{align*}\] If we multiply the two side lengths of our rectangle, we find its area. We therefore have \[\begin{align*} \text{area} &=AB \times BC \\ &= 2\sqrt{10} \times 4\sqrt{10} \\ &= 8\times10 \\ &= 80. \end{align*}\]

Here you can see a complete sketch of the rectangle.