Can we find the coordinates of this tilted rectangle?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

In the rectangle \(ABCD\), \(A\) and \(B\) are the points \((4,2)\) and \((2,8)\) respectively.

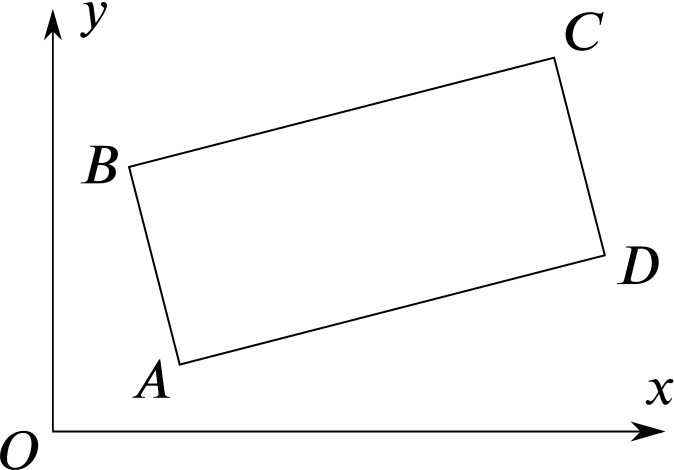
This question needs an exact method that goes beyond accurate drawing.

Given that the equation \(AC\) is \(y=x-2\), find

1. the equation of \(BC\),

If we know that \(BC\) is perpendicular to \(AB\), what can we say about the gradients of these lines?

2. the coordinates of \(C\),

We know the equations of \(BC\) and \(AC\) now…

4. the area of the rectangle \(ABCD\).

How do we calculate the area of a rectangle?