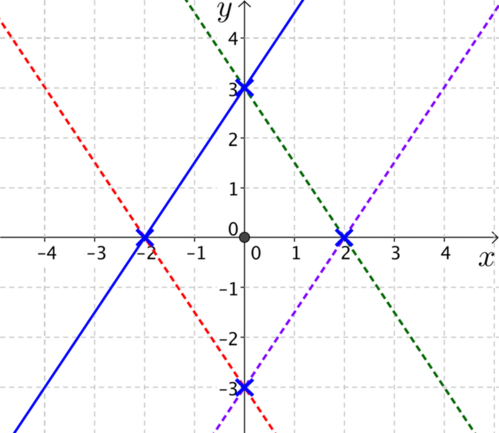
Construct a pair of straight lines whose \(x\)-intercepts differ by \(2\), \(y\)-intercepts differ by \(3\) and gradients differ by \(1\).
Is there more than one way to do this?
We might start by thinking about the specific case of a line going through the origin. We can then fix two points on a second line such that the \(x\)-intercepts differ by \(2\) and the \(y\)-intercepts differ by \(3\).
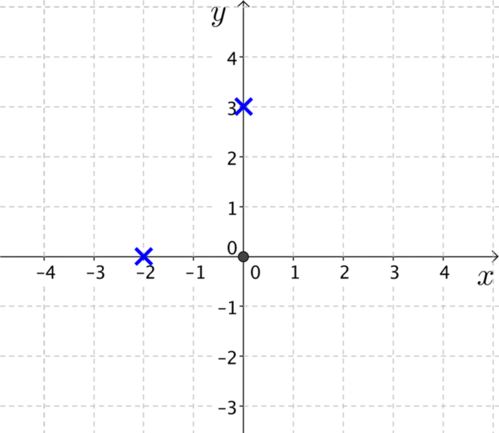
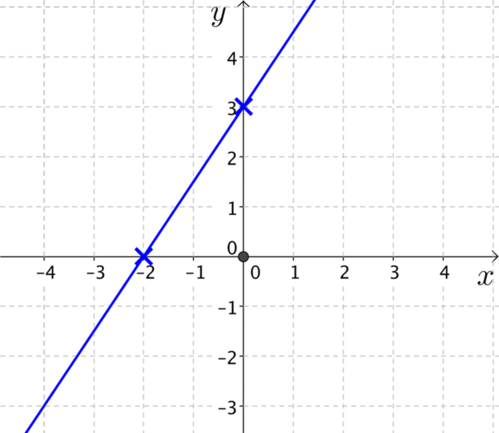
The final condition is that the gradients of the two lines differ by 1.
What is the gradient of the blue line?
Can you explain why the black line is a possible solution in each of the graphs below?
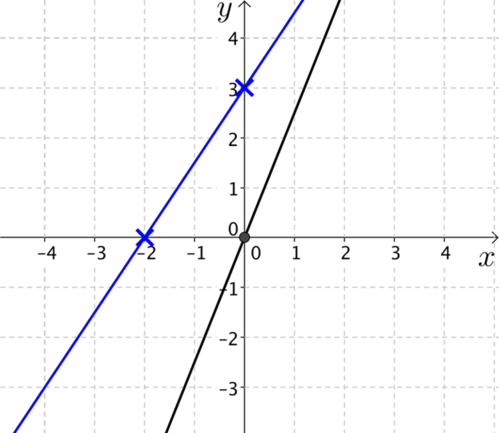
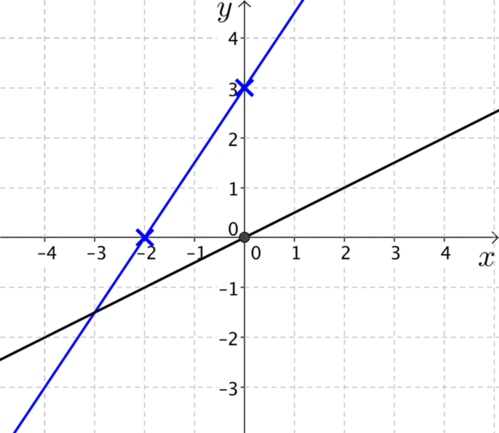
- What are the equations of each pair of lines?
This was a starting point that has successfully answered the question above, as we have already found two different solutions. We might now wonder …
Are there any other pairs that you can create with a line through the origin as a starting point?
How many pairs of lines are there in total?
Trying to solve a problem by considering a specific case such as this, is often only the first step. The next step would be to try and generalise your findings. Some of the questions we could ask ourselves would be:
- Will this method work if the line doesn’t go through the origin?
We have found several pairs of lines that share a common feature, in this case, that one of the lines passes through the origin.
Do you notice any symmetry appearing in your solutions?
Do you think you will always be able to group pairs of lines together by a common \(y\) intercept?
What other common features could you use to group pairs together?
Once you have thought about this, have a look at the Taking it further section.