Please be aware that this resource is still in a somewhat draft form.
The shape a heavy rope or chain hangs in is called a catenary. What is the equation of a catenary, and how could we work it out?
There are multiple ways to solve this problem; we’ll explore two of them.
Setting up the problem: Tension in a rope
(If you have not learnt about tension, you can just use the result from this section in the following sections.)
This diagram shows a rope hanging. We have drawn axes so that the rope hangs in the \((x,y)\)-plane with the \(y\)-axis vertically upwards and the lowest point of the rope on the \(y\)-axis.
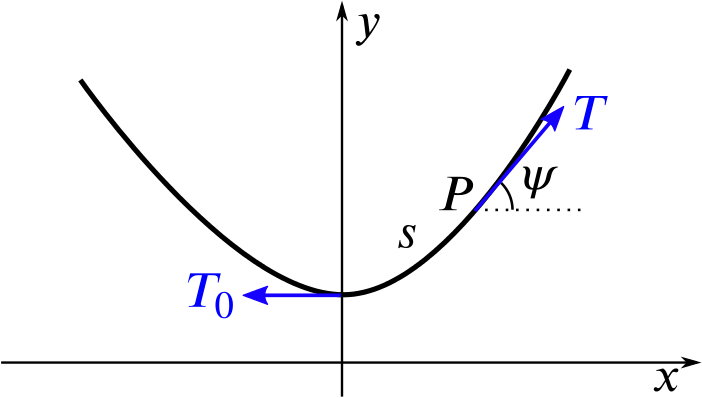
Here, \(T_0\) is the tension at the lowest point of the rope, while \(T\) is the tension at a point \(P\) which is at a distance of \(s\) along the rope from the lowest point. At \(P\), the rope makes an angle of \(\psi\) with the horizontal.
The rope has weight \(w\) per unit length.
Prove that \(\tan\psi=\Bigl(\dfrac{w}{T_0}\Bigr)s\).
From now on, we’ll make our life easier by assuming that \(w/T_0=1\), so that the equation becomes \(\tan\psi=s\).
This is a legitimate thing to do since we have not specified a unit for \(w\) (which is constant for any particular rope) and \(T_0\) is a constant for any particular situation, so we could choose a unit for measuring \(w\) which made \(w/T_0=1\).
If you want to be more general, you could still simplify things by writing \(w/T_0=1/a\), so that the equation becomes \(\tan\psi=s/a\). But the remainder of this task is tricky enough without this additional complication, so we will stick to the case \(a=1\).
If the rope has the equation \(y=f(x)\), prove that \(f'(x)=s\).
An iterative approach
We’ll start by assuming a very simple (wrong) formula for the rope length \(s\), use that to work out a first approximation for \(f(x)\), and improve it step-by-step.
We will also assume that the rope has a \(y\)-intercept of \(1\).
Step 1
Assume that \(s=x\), that is, assume the weight is evenly distributed horizontally. (This is the case for ropes holding up bridges.)
What is \(f_1(x)\) in this case, where \(f'_1(x)=s\)?
Step 2
Now assume that the weight is distributed uniformly along the shape given by the answer to Step 1, that is to say, \(s\) is now the arc length of \(y=f_1(x)\).
What is \(f_2(x)\) approximately in this case, where \(f'_2(x)=s\)? Work out an answer as a polynomial, valid for small values of \(x\), including one term more than in \(f_1(x)\).
(We’re looking for an approximation, so do not try to use any complicated integration techniques here – the most you should have to integrate is a polynomial. See the suggestions if you want one.)
Step 3
Now assume that the weight is distributed uniformly along the shape given by the answer to Step 2, that is to say, \(s\) is now the arc length of \(y=f_2(x)\).
What is \(f_3(x)\) approximately in this case, where \(f'_3(x)=s\)? Work out an answer as a polynomial, valid for small values of \(x\), including one term more than in \(f_2(x)\).
In the limit
Can you predict \(f_4(x)\)? What about \(f_5(x)\)? And how will the sequence of polynomials \(f_1(x)\), \(f_2(x)\), \(f_3(x)\), … continue further?
What is the power series, \(f(x)\), that this sequence is tending to? What do we call this function?
Can you prove that this limit function \(f(x)\) satisfies the equation \(f'(x)=s\), where \(s\) is the arc length of \(y=f(x)\)?
In the above procedure, what would Step \(n\) have been? Can you prove that Step \(n\) would have given the function \(f_n(x)\) which you predicted?
(See the suggestions for help on this step if you need it.)
Why do you think we assumed that the curve has a \(y\)-intercept of \(1\)?
A direct approach
Can you solve the equation \(f'(x)=s\) directly?
More generally, can you solve the equation \(f'(x)=\dfrac{s}{a}\), where \(f(0)=a\)?

