Setting up the problem: Tension in a rope
This diagram shows a rope hanging. We have drawn axes so that the rope hangs in the \((x,y)\)-plane with the \(y\)-axis vertically upwards and the lowest point of the rope on the \(y\)-axis.
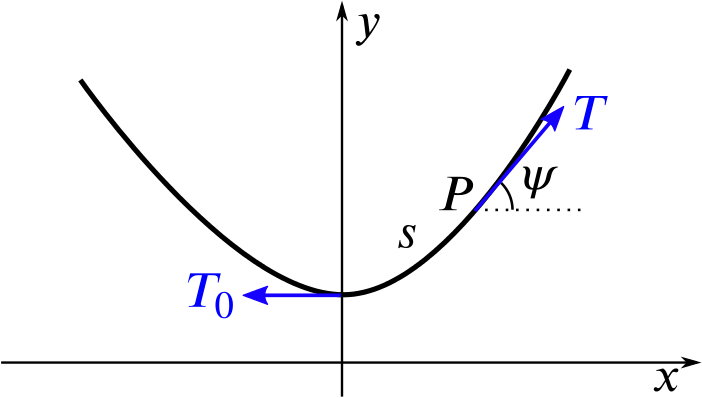
Here, \(T_0\) is the tension at the lowest point of the rope, while \(T\) is the tension at a point \(P\) which is at a distance of \(s\) along the rope from the lowest point. At \(P\), the rope makes an angle of \(\psi\) with the horizontal.
The rope has weight \(w\) per unit length.
Prove that \(\tan\psi=\Bigl(\dfrac{w}{T_0}\Bigr)s\).
(The weight of the rope is its length \(s\) times the weight per unit length \(w\).) Rearranging to get \(T\sin\psi=ws\) and \(T\cos\psi=T_0\), we can divide to get \(\tan\psi=\Bigl(\dfrac{w}{T_0}\Bigr)s\) as required.
From now on, we’ll make our life easier by assuming that \(w/T_0=1\), so that the equation becomes \(\tan\psi=s\).
If the rope has the equation \(y=f(x)\), prove that \(f'(x)=s\).
The gradient of the curve at \(P\) is \(f'(x)=\tan\psi\), so this follows immediately from \(\tan\psi=s\).
An iterative approach
We’ll start by assuming a very simple (wrong) formula for the rope length \(s\), use that to work out a first approximation for \(f(x)\), and improve it step-by-step.
We will also assume that the rope has a \(y\)-intercept of \(1\).
Step 1
Assume that \(s=x\), that is, assume the weight is evenly distributed horizontally. (This is the case for ropes holding up bridges.)
What is \(f_1(x)\) in this case, where \(f'_1(x)=s\)?
Using \(s=x\), we can integrate \(f'_1(x)=x\) to get \(f_1(x)=\frac{1}{2}x^2+c\). Using \(f_1(0)=1\), we get \(f_1(x)=1+\frac{1}{2}x^2\).
Step 2
Now assume that the weight is distributed uniformly along the shape given by the answer to Step 1, that is to say, \(s\) is now the arc length of \(y=f_1(x)\).
What is \(f_2(x)\) approximately in this case, where \(f'_2(x)=s\)? Work out an answer as a polynomial, valid for small values of \(x\), including one term more than in \(f_1(x)\).
The relevant version of the formula for arc length in this context is \[\int\sqrt{1+(f'_1(x))^2}\,dx=\int\sqrt{1+x^2}\,dx.\]
We would like a polynomial approximation to this, so we expand the square root using the binomial theorem: \[\begin{align*} \sqrt{1+x^2}&=(1+x^2)^{\frac{1}{2}}\\ &=1+\frac{1}{2}x^2+\frac{(\frac{1}{2})(-\frac{1}{2})}{2!}(x^2)^2+\cdots\\ &=1+\frac{1}{2}x^2-\frac{1}{8}x^4+\cdots \end{align*}\]So integrating gives us a formula for \(s\): \[s=x+\frac{1}{6}x^3-\frac{1}{40}x^5+\cdots\] Finally, we can now solve the equation \(f'_2(x)=s\), where \(f_2(0)=1\), to get \[f_2(x)=1+\frac{1}{2}x^2+\frac{1}{24}x^4-\frac{1}{240}x^6+\cdots\] We only want one term more than \(f_1(x)\), though, so we get \[f_2(x)=1+\frac{1}{2}x^2+\frac{1}{24}x^4.\]
Step 3
Now assume that the weight is distributed uniformly along the shape given by the answer to Step 2, that is to say, \(s\) is now the arc length of \(y=f_2(x)\).
What is \(f_3(x)\) approximately in this case, where \(f'_3(x)=s\)? Work out an answer as a polynomial, valid for small values of \(x\), including one term more than in \(f_2(x)\).
We follow the same procedure as in step 2.
We start by finding \(s\), working up to the term in \(x^4\): \[\begin{align*} s &= \int\sqrt{1+(f'_2(x))^2}\,dx\\ &= \int\sqrt{1+(x+\tfrac{1}{6}x^3)^2}\,dx\\ &= \int 1+\frac{1}{2}(x+\tfrac{1}{6}x^3)^2+ \frac{(\frac{1}{2})(-\frac{1}{2})}{2!}(x+\tfrac{1}{6}x^3)^4+\cdots\\ &= \int 1+\frac{1}{2}(x^2+\tfrac{2}{6}x^4+\tfrac{1}{36}x^6)- \frac{1}{8}(x^4+\cdots)+\cdots\\ &= \int 1+\frac{1}{2}x^2+\frac{1}{24}x^4+\cdots\\ &= x+\frac{1}{6}x^3+\frac{1}{120}x^5+\cdots \end{align*}\]and since \(f'_3(x)=s\), it follows that \[f_3(x)=1+\frac{1}{2}x^2+\frac{1}{24}x^4+\frac{1}{720}x^6= 1+\frac{x^2}{2!}+\frac{x^4}{4!}+\frac{x^6}{6!},\] giving one term more than for \(f_2(x)\).
In the limit
- Following the pattern, it would seem likely that \[\begin{align*} f_4(x)&=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\frac{x^6}{6!}+ \frac{x^8}{8!}\\ f_5(x)&=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\frac{x^6}{6!}+ \frac{x^8}{8!}+\frac{x^{10}}{10!}\\ \dots\\ f_n(x)&=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots+\frac{x^{2n}}{(2n)!}\\ \end{align*}\]
Can you predict \(f_4(x)\)? What about \(f_5(x)\)? And how will the sequence of polynomials \(f_1(x)\), \(f_2(x)\), \(f_3(x)\), … continue further?
What is the power series, \(f(x)\), that this sequence is tending to? What do we call this function?
It appears to be \[f(x)=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots+\frac{x^{2n}}{(2n)!}+ \cdots\]
This function is \(\cosh x\), the hyperbolic cosine. It is defined either by this power series or by the identity \[\cosh x=\frac{e^x+e^{-x}}{2}.\]
Interestingly, this power series is valid for all values of \(x\), not only values less than \(1\).
- The limit function, \(y=f(x)=\cosh x\), has arc length from \(0\) to \(x\) given by \[\begin{align*} s&=\int_0^x \sqrt{1+(f'(x))^2}\,dx\\ &=\int_0^x \sqrt{1+(\sinh x)^2}\,dx\\ &=\int_0^x \cosh x\,dx\\ &=[\sinh x]_0^x\\ &=\sinh x \end{align*}\]
Can you prove that this limit function \(f(x)\) satisfies the equation \(f'(x)=s\), where \(s\) is the arc length of \(y=f(x)\)?
And \(f'(x)=\sinh x\), so \(f'(x)=s\).
We have been a bit sloppy with notation here, using \(x\) as both one of the limits and also as the variable in the integral. If we were to be more careful, we would have changed the variable in the integral to a different letter such as \(t\).
In the above procedure, what would Step \(n\) have been? Can you prove that Step \(n\) would have given the function \(f_n(x)\) which you predicted?
Step \(n\) would read:
“Now assume that the weight is distributed uniformly along the shape given by the answer to Step \(n-1\), that is to say, \(s\) is now the arc length of \(y=f_{n-1}(x)\).
What is \(f_n(x)\) approximately in this case, where \(f'_n(x)=s\)? Work out an answer as a polynomial, valid for small values of \(x\), including one term more than in \(f_{n-1}(x)\)."
Since the construction is by iteration, the proof is by induction.
We assume that the previous step (Step \(n-1\)) gave us the expected function, that is, we assume that \[f_{n-1}(x)=1+\dfrac{x^2}{2!}+\cdots+\dfrac{x^{2(n-1)}}{(2(n-1))!}.\] Then to find \(f_n(x)\), we begin by working out the arc length of \(y=f_{n-1}(x)\) from \(0\) to \(x\): \[s=\int_0^x \sqrt{1+(f'_{n-1}(x))^2}\,dx.\] But this integral is going to be very hard to calculate directly: we will need to differentiate \(f_{n-1}(x)\), square it, and then use the binomial theorem to expand the square root.
However, we can use what we know about \(f_{n-1}(x)\) to sidestep many of these difficulties: \(f_{n-1}(x)\) is the expansion of \(\cosh x\) up to the term in \(x^{2n-2}\).
Therefore, \(f'_{n-1}(x)\) is the expansion of \(\sinh x\) up to the term in \(x^{2n-3}\). (We can work this out directly by differentiating \(f_{n-1}(x)\) if we wish.) In fact, it even agrees up to the term in \(x^{2n-2}\), which is zero.
Therefore \(1+(f'_{n-1}(x))^2\) will agree with the expansion of \(1+\sinh^2 x=\cosh^2 x\) up to at least the term in \(x^{2n-2}\).
When we then use the binomial theorem to expand \(\sqrt{1+(f'_{n-1}(x))^2}\) as a power series in \(x\), it will have to agree with \(\cosh x\) up to at least the term in \(x^{2n-2}\), since the expression inside the square root agrees up to at least this term.
Thus when we integrate this to get \(f'_n(x)=s\), it will agree with \(\int\cosh x\,dx=\sinh x\) up to at least the term in \(x^{2n-1}\). (And the constant term in the integral is zero, as the integral is from \(0\) to \(x\), which agrees with the zero constant term in the expansion of \(\sinh x\).)
Then we integrate this final expression to get \(f_n(x)\), so this will agree with \(\int\sinh x\,dx=\cosh x\) up to at least the term in \(x^{2n}\), and the constant term is also correct as \(f_n(0)=1\).
Since we let \(f_n(x)\) be the polynomial with just one term more than \(f_{n-1}(x)\), we find that \(f_n(x)\) is the polynomial approximation to \(\cosh x\) with terms up to \(x^{2n}\), that is, \[f_n(x)=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots+\frac{x^{2n}}{(2n)!}\] as we wanted.
- The limiting function is \(\cosh x\), and \(\cosh 0=1\). Had we chosen a different \(y\)-intercept, say \(0\), the limiting function would have been \(\cosh x-1\), which would have been a little bit less pretty.
Why do you think we assumed that the curve has a \(y\)-intercept of \(1\)?
A direct approach
Can you solve the equation \(f'(x)=s\) directly?
Using the formula for arc length, this differential equation becomes \[f'(x)=\int_0^x \sqrt{1+(f'(t))^2}\,dt.\] (Here we’re being good and not using \(x\) as the variable in the integration, to avoid confusing ourselves.) This equation may seem very hard at first, but we might notice that \(f(x)\) itself never appears, just its derivative.
So let’s write \(p(x)=f'(x)\), to get \[p(x)=\int_0^x \sqrt{1+(p(t))^2}\,dt,\] which looks marginally simpler as there’s no differentiation involved.
We still have this pesky integral, but we can get rid of that by differentiating both sides with respect to \(x\), and making use of the fundamental theorem of calculus: \[p'(x)=\sqrt{1+(p(x))^2}.\] No integral left!
We could try squaring both sides to get rid of the square root, but then we’d have \((p'(x))^2\), a squared derivative, which is not nice.
If we write \(p'(x)\) as \(\frac{dp}{dx}\) things might look more familiar (and we’ll write \(p\) in place of \(p(x)\), too): \[\frac{dp}{dx}=\sqrt{1+p^2}.\] This is a separable differential equation! So separating the variables, we get \[\int \frac{1}{\sqrt{1+p^2}}\,dp=\int 1\,dx.\] The right hand side is easy. For the left hand side, we use the substitution \(p=\sinh u\), so \(\frac{dp}{du}=\cosh u\), giving \[\int \frac{1}{\sqrt{1+\sinh^2 u}}\cosh u\,du=x,\] which simplifies to \[\int 1\,du=x,\] so \(u=x+c\), giving \(\arsinh p=x+c\) or \(p=\sinh(x+c)\).
Now we can also work out from our original differential equation that \(p(0)=0\), so \(c=0\) and \(p=\sinh x\).
But \(p=f'(x)\), so \(f'(x)=\sinh x\), giving \(f(x)=\cosh x+C\).
Finally, using \(f(0)=1\) gives \(C=0\), so \(f(x)=\cosh x\).
More generally, can you solve the equation \(f'(x)=\dfrac{s}{a}\)?
The argument is very similar to the above; one just has to take care with the extra \(a\) term. The solution is \(f(x)=a\cosh(\frac{x}{a})\).

