Discussing distance

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

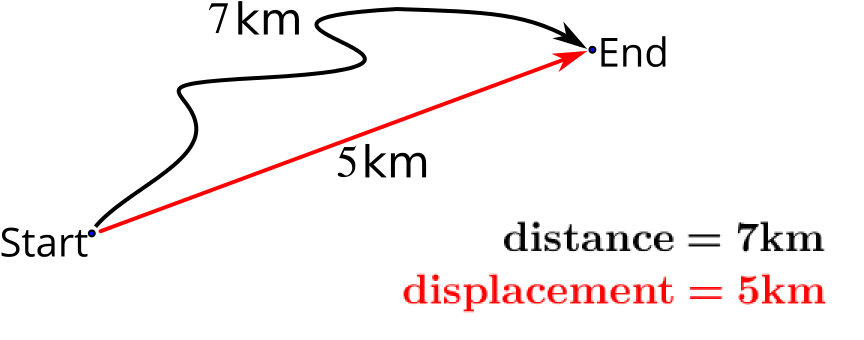
The two graphs below depict the same journey along a straight road.

• What’s the same and what’s different about the graphs?
• What do you think the labels on the each of the axes would be?

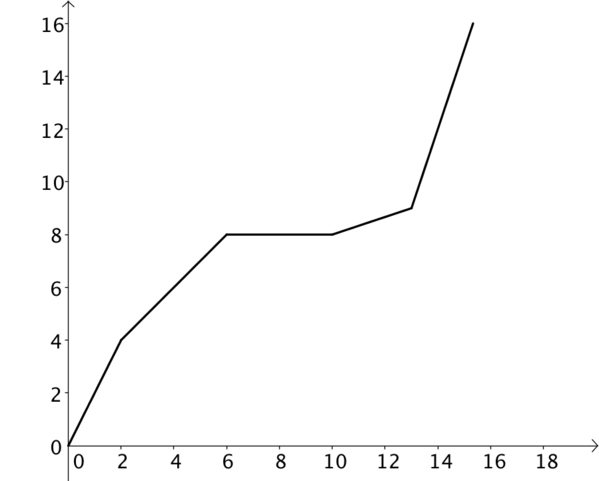
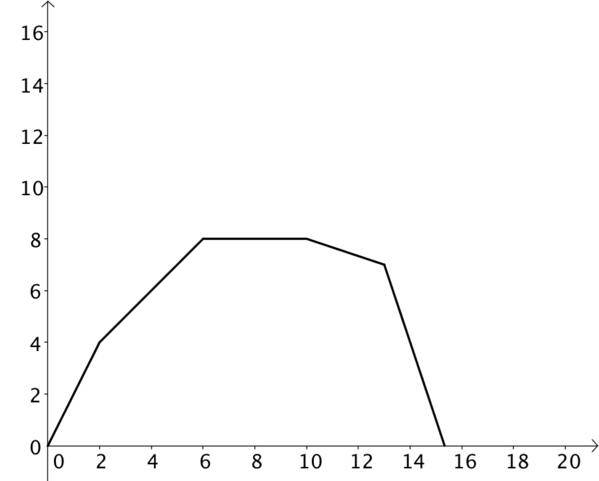
Initial ideas might have been a distance-time graph and a speed-time graph. If this were true, would it be possible for them to represent the same journey? How would a constant speed be represented on each?

If we think only about distance, we should notice that the two graphs cannot both be distance-time graphs. Distance can only go on increasing; you cannot undo the distance you have travelled. The left hand graph is a distance-time graph, but the right hand graph is something else, in this case a displacement-time graph.

Displacement explanation

If you walk \(\quantity{1.5}{km}\) to school every day then, when you have walked home, you have covered a distance of at least \(\quantity{3}{km}\) by the end of the day. However, if you talk about displacement, then by the end of the day you are back at your starting point, so your displacement is \(0\).

Distance is how much ground you have covered in your travels, whereas displacement looks at how far you are from your starting point.

If we compare the graphs, then from \(0\) to \(10\) on the \(x\) axis, our graphs are identical. After this, they differ.

• What do you think changes in the journey after this point?
• What do you notice about the gradients of the same section on each graph?