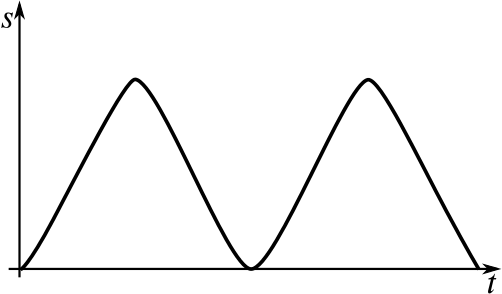
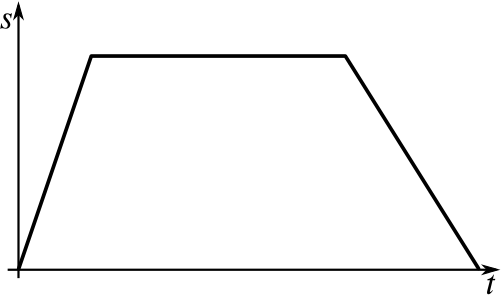
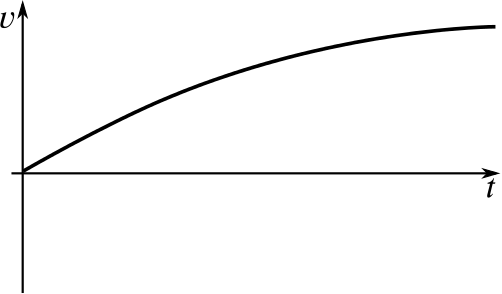
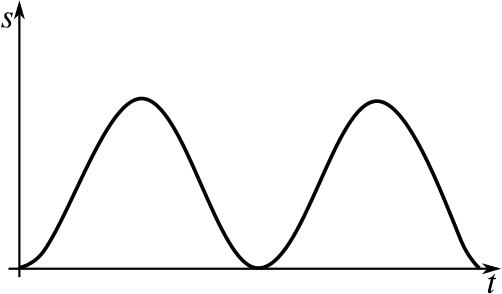
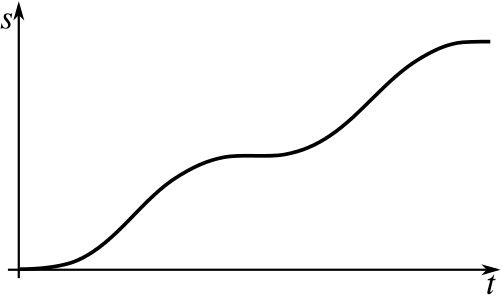
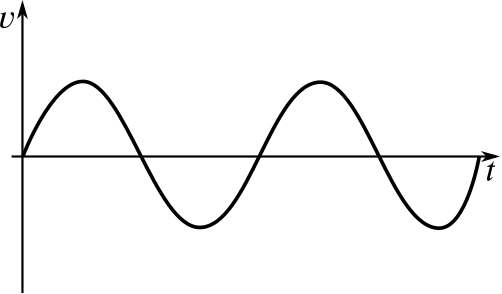
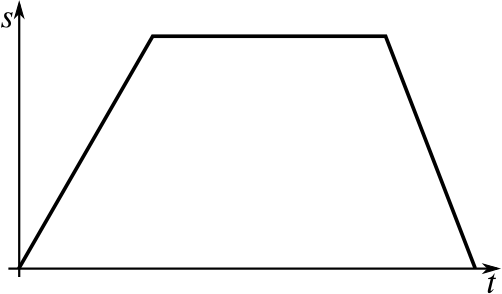
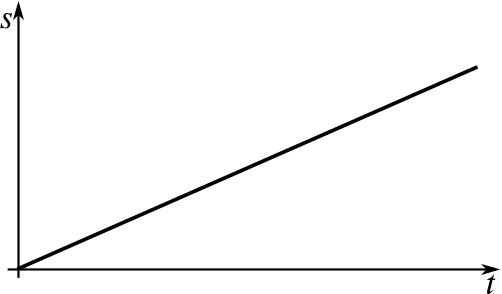
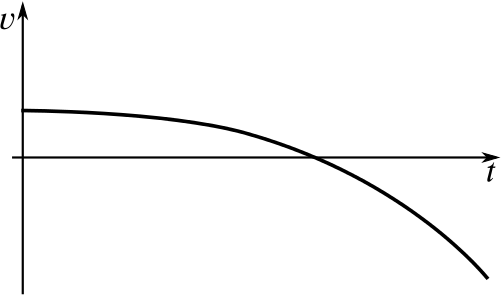
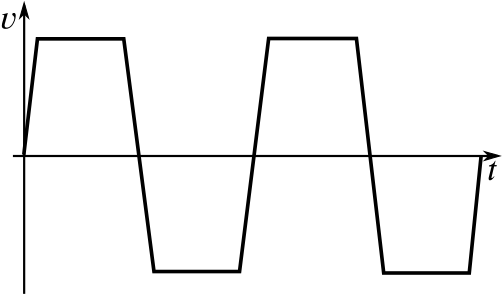
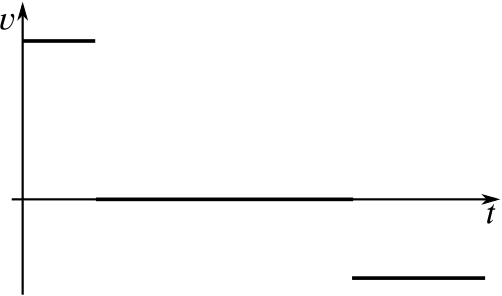
Can you match up the following displacement–time graphs with their corresponding velocity–time graphs? Some of the graphs have not been drawn; you will need to complete them yourself.
When you have matched them up, could you give descriptions of what might be happening in them? Here are some possible contexts we’ve thought of; feel free to use your own instead.
- A baby in a baby-bouncer
- A toy car being pushed or pulled
- The ribbon in a tug-of-war game
- A ball being thrown upwards
- A yo-yo
(For the distinction between displacement and distance, have a look at Discussing distance. A similar comparison between speed and velocity is found in Speed vs velocity.)