Can you match up the following displacement–time graphs with their corresponding velocity–time graphs? Some of the graphs have not been drawn; you will need to complete them yourself.
When you have matched them up, could you give descriptions of what might be happening in them?
Here is how we matched the graphs up, including the missing ones, which have been highlighted.
We’ve given a suggested context for each one, but you may well be able to do better!
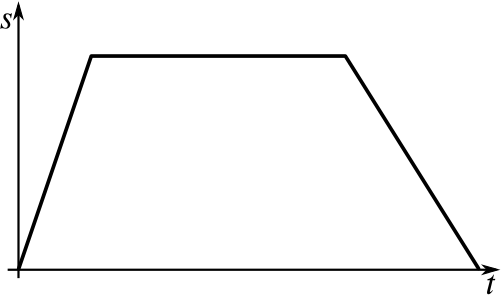
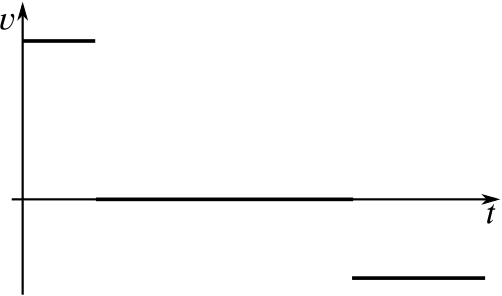
Fred runs down the road to the shop, stops to buy an ice-cream, then walks back eating it.
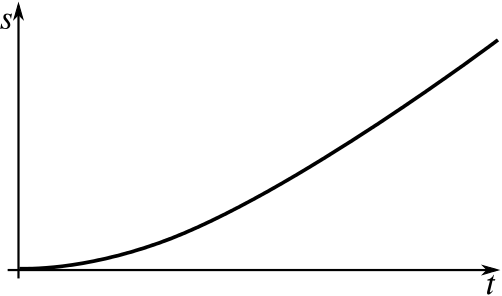
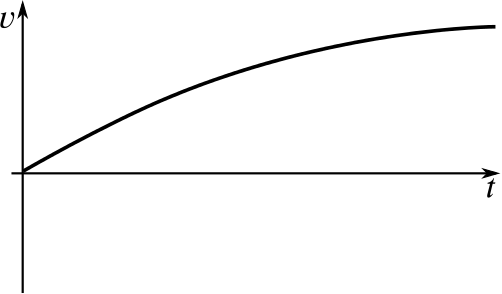
The distance–time graph starts horizontal, as the initial velocity is zero, but then it becomes steeper as the velocity increases, eventually seeming almost like a straight line.
It’s the beginning of a cycle race, and a cyclist gradually picks up speed as the race begins, until she is going at a reasonably constant speed.
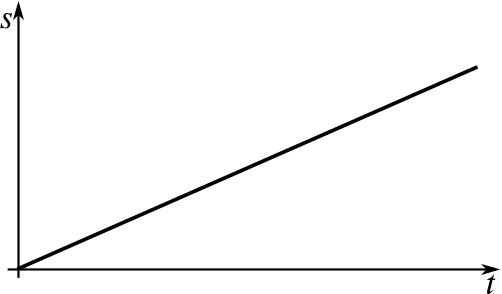

Sheena is walking along at a constant speed.
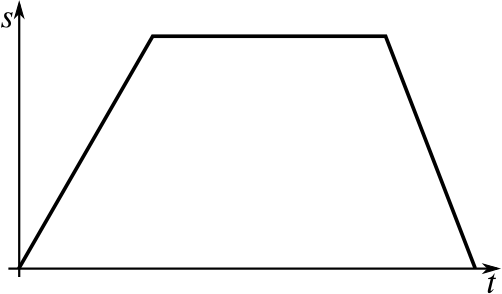
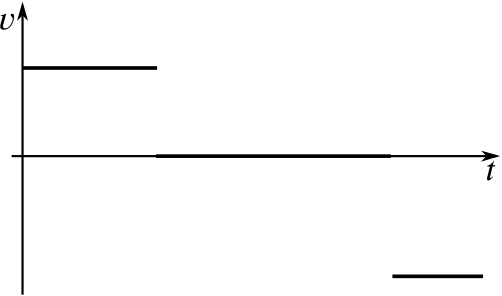
The velocity is initially positive, as the distance away is increasing, then it is zero, as the person or object is staying still, then it is negative, as the distance away is decreasing. The initial gradient has some value, say \(3\), and the final gradient is steeper, so might have a value such as \(-5\).
This might represent a dog walking with their owner, stopping while the owner has a conversation with a friend, then running back to retrieve a ball which the owner has thrown.
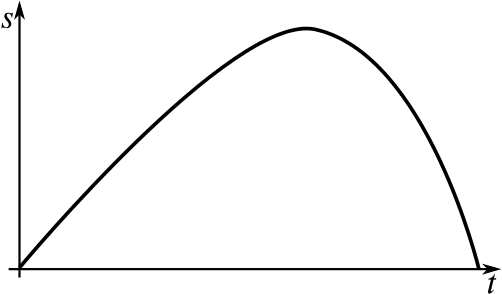
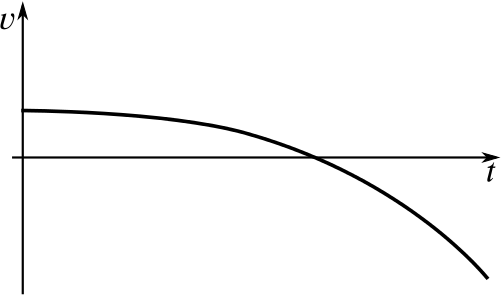
The velocity is initially positive and fairly constant, so the distance–time graph will initially be almost a straight line with positive gradient. But then the velocity reaches zero, so the person or object stops, and the distance–time graph is horizontal. Then the velocity becomes negative, so the distance decreases, more steeply than it increased.
This is Fraser’s height above the ground on an amusement park vertical-drop ride. He’s being steadily pulled up to the top of the ride, then the roller coaster is released, and he gets faster and faster. (This isn’t quite realistic, though, as the ride does need to slow down again!)
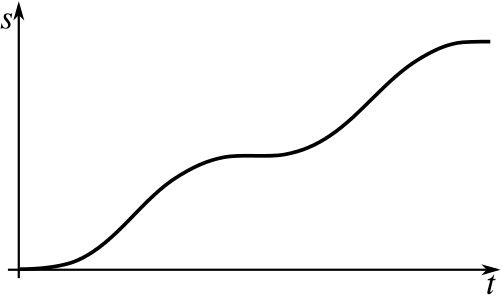
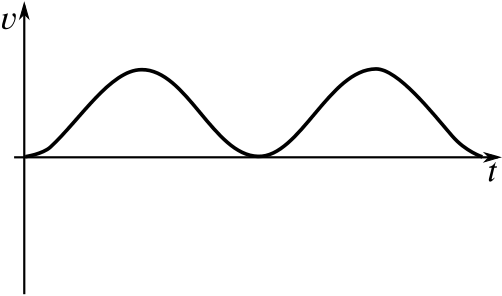
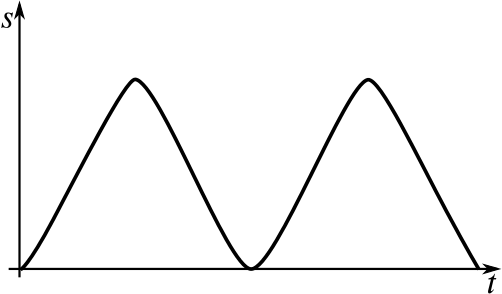
This object starts from rest, that is, the initial velocity is zero. It then increases its velocity for a bit before slowing back down to a stop. This is repeated a second time.
This could be a toy car being pulled along on a string. It is given a pull, which sets it going, but it then slows down, coming to a stop. It is then given another pull, and the same happens again.
The precise shape of the distance–time graph actually suggests that there is some sort of spring or elastic involved.
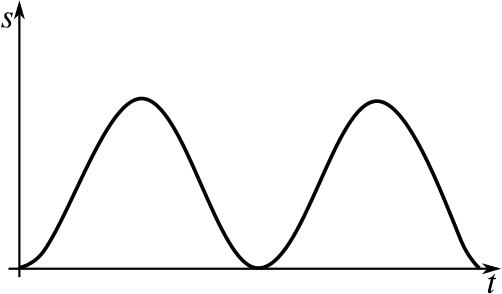
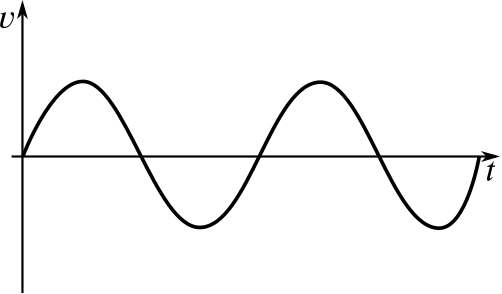
This initially looks like it could be the height of a yo-yo, but a yo-yo often jerks at its lowest point, whereas this graph is quite gentle there.
Perhaps a baby on a baby-bouncer would be a better fit? Or a jack-in-the-box bouncing? Or maybe a weight on the end of a piece of elastic bobbing up and down?
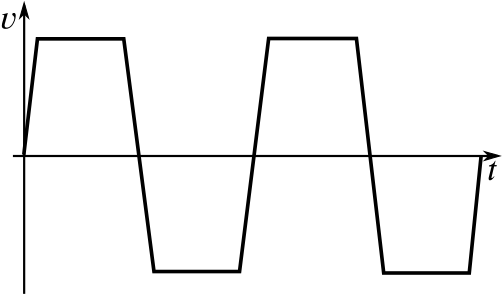
This is very similar to the last pair, but the velocity is constant at the heighest and lowest values, so the distance–time graph has straight line parts.
This could be a swimmer doing widths of a pool: they swim at a constant speed during the width, but slow down near the sides of the pool as they turn around.

