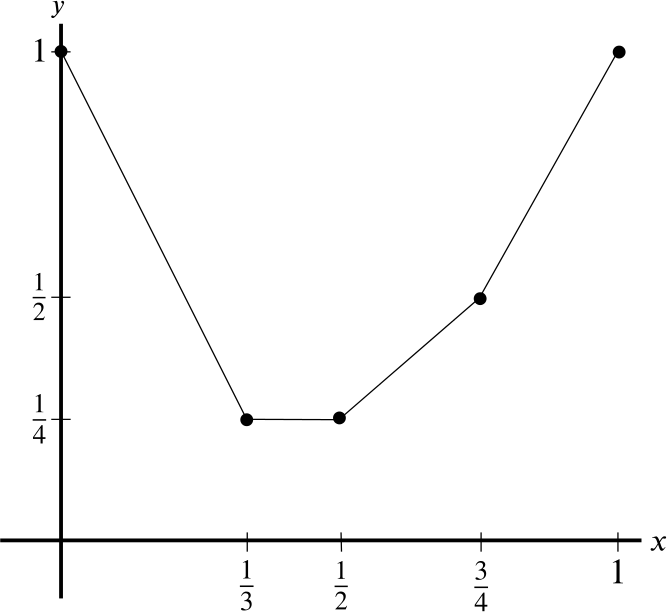
The graph \(y=f(x)\) of a function is drawn below for \(0 \le x \le 1\).
The trapezium rule is then used to estimate
\[\displaystyle\int_0^1 \! f(x) \, \mathrm{d}x\]
by dividing \(0 \le x \le 1\) into \(n\) equal intervals. The estimate calculated will equal the actual integral when
\(n\) is a multiple of \(4\);
\(n\) is a multiple of \(6\);
\(n\) is a multiple of \(8\);
\(n\) is a multiple of \(12\).
The function \(f(x)\) is linear on the intervals
\[0 \le x \le \frac{1}{3},\]
\[ \frac{1}{3} \le x \le \frac{1}{2} ,\]
\[\frac{1}{2} \le x \le \frac{3}{4},\]
\[\frac{3}{4} \le x \le 1,\]
and in order to use the trapezium rule, we need to divide the interval \(0 \le x \le 1\) into \(n\) equal intervals.
However, if the values \(x = \dfrac{1}{3}, \dfrac{1}{2}, \dfrac{3}{4}\) aren’t at the end of an interval, then the trapezium rule will overestimate the value of the integral.
For example, if we took \(\dfrac{1}{4} \le x \le \dfrac{1}{2}\) as one of the intervals (\(n=4\)), then we would be overestimating the value of the integral, because we would also be including the area of triangle A, as shown below.

Therefore we need to choose a value of \(n\) such that \(x = \dfrac{1}{3}, \dfrac{1}{2}, \dfrac{3}{4}\) lie at the end of intervals.
The largest such interval would be of width \(\dfrac{1}{12}\), that is, \(n=12\), and similarly, \(n\) can be any multiple of \(12\).
Hence the answer is (d).

