When does the trapezium rule give the exact answer here?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

The graph \(y=f(x)\) of a function is drawn below for \(0 \le x \le 1\).

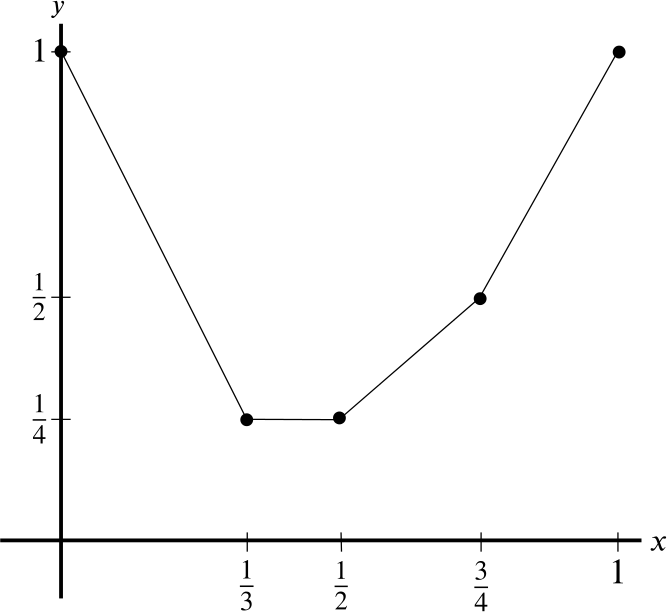
The trapezium rule is then used to estimate

\[\displaystyle\int_0^1 \! f(x) \, \mathrm{d}x\]

by dividing \(0 \le x \le 1\) into \(n\) equal intervals. The estimate calculated will equal the actual integral when

1. \(n\) is a multiple of \(4\);

2. \(n\) is a multiple of \(6\);

3. \(n\) is a multiple of \(8\);

4. \(n\) is a multiple of \(12\).

The notation \[\displaystyle\int_0^1 \! f(x) \, \mathrm{d}x\] means the area between the \(f(x)\) and the \(x\)-axis, from \(x=0\) to \(x=1\).