Fill in the blank spaces so that each row contains:
- an inequality
- a graph that can help solve the inequality
- a solution set of the inequality.
| Solution set | Graph | Inequality |
|---|---|---|
| \(\left\{x: 2<x<5\right\}\) |
One way to start might be to think about the solution set on a pair of axes, and then sketching a graph that would fit the constraints.

The graph sketched above is \(y = a(x-2)(x-5)\) where \(a>0\). For the inequality we could suggest something specific such as \((x-2)(x-5) < 0\), or we could be more general and write \(a(x-2)(x-5) < 0\).
What would happen if \(a < 0\)? How would the graph change? How would the inequality change?
| Solution set | Graph | Inequality |
|---|---|---|
| \(\left\{x: 0<x≤1\right\}\) |
Why can’t this solution set satisfy a quadratic inequality?
We want \(1\) to be included, but \(0\) is not part of the solution. What graphs can we sketch that will satisfy this constraint? Two suggestions are shown here.

|

|
Both graphs have asymptotes at the \(y\)-axis, which gives the correct solution set since the two functions don’t exist when \(x=0\).
\(y = \dfrac{1}{x^2}-1\) also has an asymptote on the \(y\)-axis and a root at \(x = 1\). Why isn’t the inequality \(\dfrac{1}{x^2}-1≥0\) a possible answer?
| Solution set | Graph | Inequality |
|---|---|---|
|
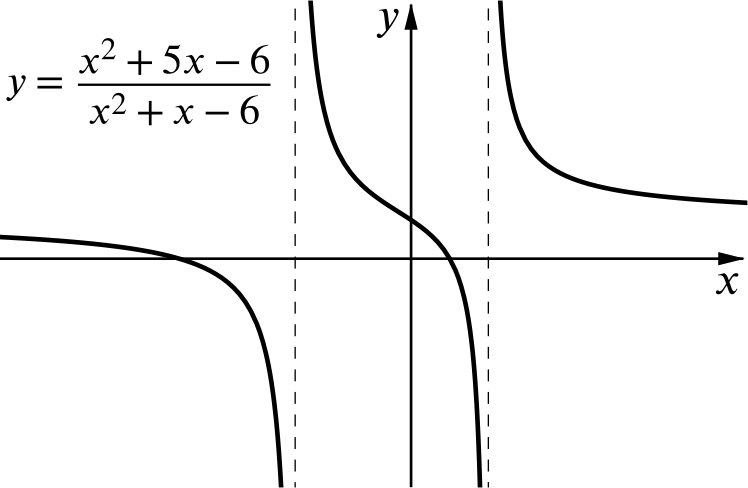
\(\dfrac{x^2+5x-6}{x^2+x-6}≥0\) |
We want to know where our graph is greater than or equal to zero. To find these sections we need to know the \(x\)-intercepts and the asymptotes.
The two asymptotes can be found by finding for what values the denominator, \(x^2 + x - 6\), equals zero, which is \(x = -3\) and \(x = 2\).
The graph will cross the \(x\)-axis when \(y = 0\), which means when \(x^2 + 5x - 6 =0\). The intercepts are at \(x = -6\) and \(x = 1\).

Therefore the solution set of \(\dfrac{x^2+5x-6}{x^2+x-6}≥0\) is \(\left\{x: x≤-6\right\} \cup \left\{x:-3<x≤1\right\}\cup \left\{x: x>2\right\}\).
| Solution set | Graph | Inequality |
|---|---|---|
| \(x^2 + 6x > 2x+1\) |
There are several different graphs we could sketch to help us solve \(x^2 + 6x > 2x+1\). Two examples are shown below.

|

|
Both examples can be sketched reasonably accurately without having to do any calculations. They give us a way to approximate solutions and enable us to see what the solution set will look like, i.e. \(\left\{x: a<x<b\right\}\) or \(\left\{x: x<a\right\}\cup \left\{x: x>b\right\}\).
What other graphs could be sketched? Are they any more or less helpful than those above?
Finding the intersection points by solving \(x^2 + 6x = 2x+1\) gives us a solution set of \(\left\{x: x<-2-\sqrt{5}\right\} \cup \left\{x: x> -2 + \sqrt{5} \right\}\).
| Solution set | Graph | Inequality |
|---|---|---|
| \(\left\{x: x<-5\right\} \cup \left\{x:-2<x<2\right\}\) |
The solution set implies that we have three values where the graph switches from positive to negative. If we interpret these as roots then we could sketch a cubic.

This is the graph of \(y = a(x+5)(x+2)(x-2)\) where \(a > 0\), so the inequality will be \(a(x+5)(x+2)(x-2) ≤ 0\).
What if the three values are not all roots? If one of them is an asymptote can you still find a graph that fits the solution set?

