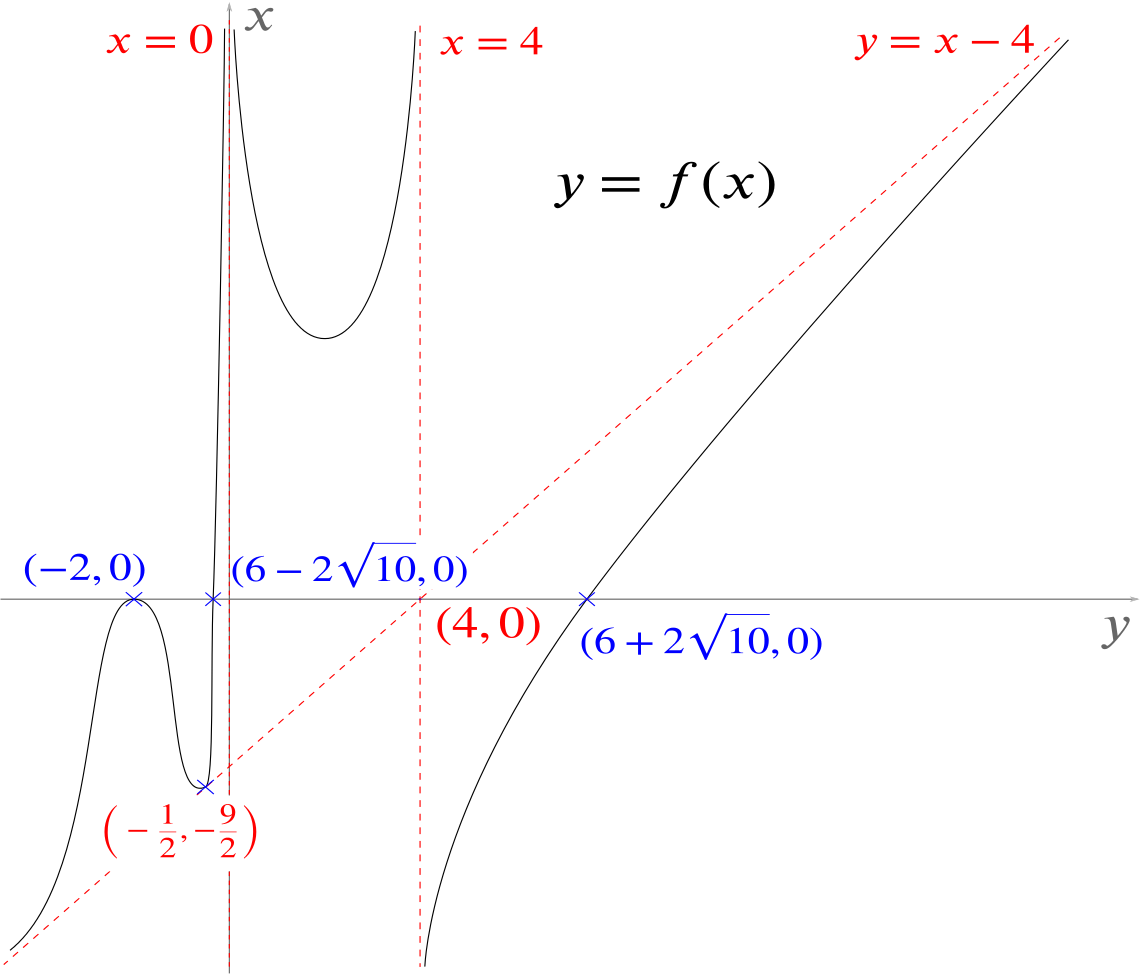
The equation of a curve is \(y=f(x)\) where \[f(x)=x-4-\frac{16(2x+1)^2}{x^2(x-4)}.\]
- Write down the equations of the vertical and oblique asymptotes to the curve and show that the oblique asymptote is a tangent to the curve.
Inspecting the equation for \(f(x)\), we can see that we have vertical asymptotes when \(x=0\) and \(x=4\).
We also see that as \(x\to\pm\infty\), the fractional term will get closer and closer to zero, so that \(f(x)\) will look more and more like \(y=x-4\), so this is the oblique asymptote.
We want to show that \(y=x-4\) is tangent to the curve. We first check whether \(y=x-4\) and \(y=f(x)\) intersect. We have \[\begin{align*} & x-4 = x-4-\frac{16(2x+1)^2}{x^2(x-4)} \\ \iff & \frac{16(2x+1)^2}{x^2(x-4)}=0. \end{align*}\]This happens when \((2x+1)=0\), that is, when \(x=-1/2\), which gives \(y = -\dfrac{9}{2}\).
Since the \(2x+1\) factor is squared in \(\dfrac{16(2x+1)^2}{x^2(x-4)}=0\), we have a double root, and the curve touches the oblique asymptote at \(\left(-\dfrac{1}{2}, -\dfrac{9}{2}\right)\).
- Show that the equation \(f(x)=0\) has a double root.
Setting \(f(x)=0\) and multiplying through by \(x^2(x-4)\), we find \[x^2(x-4)^2-16(2x+1)^2=0.\]
It might be tempting here to just expand the brackets, however, that will leave us with a quartic, which is going to be quite difficult to factorise by inspection.
However, we can notice that the expression is of the form \(a^2-b^2\), where \(a\) and \(b\) are both quadratics.
So we can use the fact that \(a^2-b^2=(a-b)(a+b)\), which will be much easier to factorise.
This is known as the difference of two squares, and is a good way of saving time.
and so we see that \(f(x)=0\) has a double root at \(x=-2\).
- Sketch the curve.
We have found much information about the curve from parts (i) and (ii).
We can sketch on the axis where the asymptotes are, where the curve meets the \(x\) axis (and indeed where it doesn’t), and where it meets the line \(y=x-4\).
By carefully inspecting \(y=f(x)\), we can also tell whether it tends to \(\pm \infty\) by considering whether \(f(x)\) is positive or negative when \(x\) is close to \(0\) and \(4\).
Remember to check both sides of an asymptote, because it won’t necessarily come back from infinity the same way it went up!
We need to be a bit careful when sketching where the curve is tangent to \(y=x-4\)—this definitely isn’t a stationary point, since we worked out in part (i) that the gradient at this point was \(1\).
We can now sketch the curve.