Which one of the following equations could possibly have the graph given below?
- \(y = (3-x)^2(3+x)^2(1-x)\);
- \(y = -x^2(x-9)(x^2-3)\);
- \(y = (x-6)(x-2)^2(x+2)^2\);
- \(y = (x^2-1)^2(3-x)\).
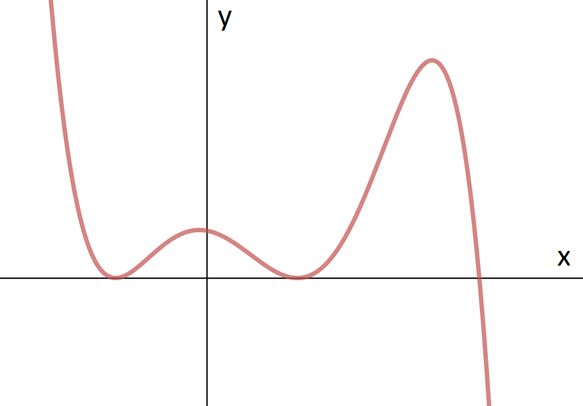
All four of the equations given here are quintics (having \(x^5\) as the highest power of \(x\)), and this fits with the graph which has four turning points.
The sketch shows that \(y\to-\infty\) as \(x\to\infty\), so the coefficient of the highest power of \(x\) must be negative.
This eliminates (c), as its coefficient of \(x^5\) is positive. Alternatively, the graph tells us that when \(x=0\), \(y>0\), but for (c), \(y<0\), which also eliminates (c).
The graph we are given has two repeated roots (where the graph touches the \(x\)-axis). A repeated root at \(x=a\) will appear as \((x-a)^2\) (or a higher power of this) in the equation.
This eliminates (b). Alternatively, we can eliminate (b) as it would pass through the origin.
The graph’s repeated roots are the smallest and middle ones, which eliminates (a) (because its smallest and largest roots are repeated).
Hence the answer is (d), which can be written as \[y=\bigl((x+1)(x-1)\bigr)^2(3-x)=(x+1)^2(x-1)^2(3-x),\] so it has repeated roots at \(-1\) and \(+1\) and its largest root at \(3\).

