Which of these quintic equations fit this graph?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Which one of the following equations could possibly have the graph given below?

1. \(y = (3-x)^2(3+x)^2(1-x)\);

2. \(y = -x^2(x-9)(x^2-3)\);

3. \(y = (x-6)(x-2)^2(x+2)^2\);

4. \(y = (x^2-1)^2(3-x)\).

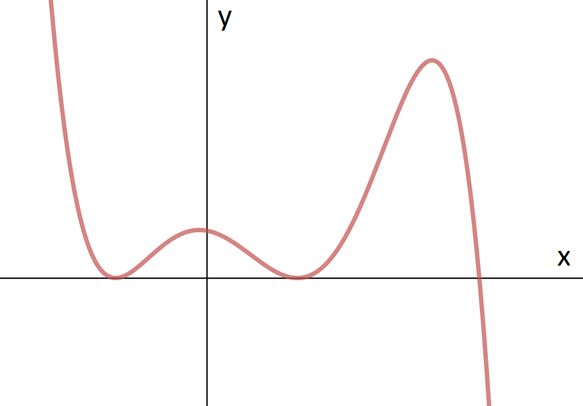
If the curve touches the \(x\)-axis at \(x=a\), what do we know about the equation of the curve?

What happens as \(x\) approaches \(\pm \infty\) for each of these equations?