A spherical planet of radius \(a\) has a variable density \(f(r)\) which depends only on the distance \(r\) from the planet’s centre. Show that the average density of the planet is \[3 \int_0^1 t^2 f(at) \:dt.\]
Let’s consider the hollow sphere of radius \(r\), where \(r < a\), and thickness \(\delta r\), as shown below.
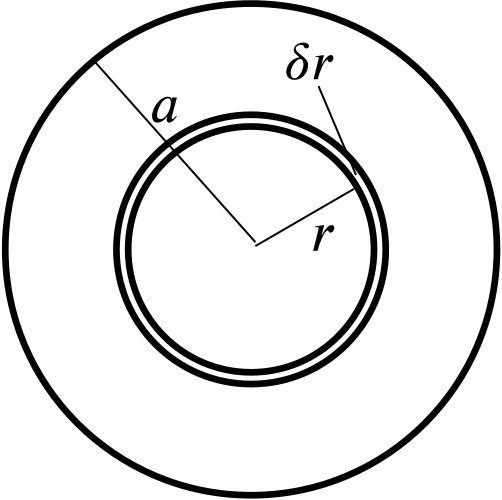
The volume of this hollow sphere is \(\delta V = \dfrac{4\pi}{3}(r + \delta r)^3 - \dfrac{4\pi}{3}r^3= 4\pi r^2 \delta r\) (neglecting higher powers of \(\delta r\)).
Alternatively, \(\delta V =\) surface area of the hollow sphere\(\times\) its thickness.
We know that the density of this hollow sphere is \(f(r)\), so the mass of the hollow sphere is \(4\pi r^2 f(r) \delta r\).
Taking the limit, the total mass of the whole sphere is therefore
\[\int_0^a 4\pi r^2 f(r) \:dr.\]
We know that the volume of the whole sphere is \(\dfrac{4\pi}{3}a^3\), so the average density of the whole sphere is \[\dfrac{\int_0^a 4\pi r^2 f(r) \:dr}{\frac{4\pi}{3}a^3}\] which is \[\int_0^a \dfrac{3 r^2 f(r)}{a^3} \:dr.\]
If we now put \(r = at\), we have \(dr = a\: dt\), and substituting in, we find that the average density is \[3 \int_0^1 t^2 f(at) \:dt,\] as required.
Find the average density correct to two significant figures in each of the three cases:
- \(f(r) = \exp\left[\left(-\dfrac{r}{a}\right)^3\right]\), where \(\exp(x)\) denotes \(e^x\),
Our work from the first part tells us that we need to find the following integral, which we can do by inspection or by substitution.
\[\begin{align*} \int_0^1 3t^2 e^{-t^3} \:dt &=\left[-e^{-t^3}\right]_0^1\\ &=1-e^{-1}\\ &=0.63 \quad (2\text{sf}). \end{align*}\]- \(f(r) = \exp\left(-\dfrac{r}{a}\right)\),
Using the first part again tells us that we need to find the following. This time we use integration by parts twice.
\[\begin{align*} \int_0^1 3t^2 e^{-t} \:dt &= 3\Big[-t^2e^{-t}\Big]_0^1 - 3\int_0^1 -e^{-t}2t \:dt\\ &=-3e^{-1} +6\int_0^1te^{-t}\:dt \\ &=-3e^{-1} +6\left\{ \Big[-te^{-t}\Big]_0^1 - \int_0^1-e^{-t}\:dt \right\}\\ &=-9e^{-1} -6\Big[e^{-t}\Big]_0^1 \\ &=-15e^{-1} + 6\\ &= 0.48 \quad (2\text{sf}). \end{align*}\]- \(f(r) = \dfrac{a^2r}{(a+r)^3}\).
Once again we can use the first part so that we need to find \[\int_0^1 \dfrac{3t^3}{(1+t)^3} \:dt.\]
Let’s use partial fractions to write \(\dfrac{t^3}{(1+t)^3}\) as \(A + \dfrac{B}{1+t} + \dfrac{C}{(1+t)^2} + \dfrac{D}{(1+t)^3}\). Putting all this over a common denominator gives \[\begin{align*} \dfrac{t^3}{(1+t)^3} &= \dfrac{A(1+t)^3+B(1+t)^2+C(1+t)+D}{(1+t)^3} \\ &= \dfrac{At^3+(3A+B)t^2+(3A+2B+C)t+(A+B+C+D)}{(1+t)^3}, \end{align*}\] which gives us on comparing coefficients \(A = 1\), \(B = -3\), \(C = 3\), \(D = -1\). So our integral becomes \[\begin{align*} &3\int_0^1 1 -\dfrac{3}{1+t} + \dfrac{3}{(1+t)^2}-\dfrac{1}{(1+t)^3} \:dt\\ &= 3\left[t-3\ln(1+t)-3\dfrac{1}{1+t} +\dfrac{1}{2(1+t)^2}\right]_0^1\\ &= 3\left(1-3\ln2-\dfrac{3}{2} + \dfrac{1}{8}\right)-3\left(-3+\dfrac{1}{2}\right)\\ &= 3(2.125-3\ln2) \\ &= 0.14 \quad (2\text{sf}). \end{align*}\]Alternatively, rather than using partial fractions, we could write \(u=1+t\) so that our integral becomes \[3\int_1^2 \frac{(u-1)^3}{u^3}\:du\] which we can expand, cancel and integrate as powers of \(u\) with the same result as above.

