where \(p>0\), \(p\ne r\) and \(n=1\), \(2\), \(3\), \(\dots\).
- For the case where \(p=3\), \(q=50\), \(r=2\), \(s=15\), find the set of values of \(n\) for which equation \(\eqref{eq:starrepeat}\) has no real roots.
has no real roots.
We therefore want to determine the values of \(n\) for which the discriminant is negative, that is, \(n\) such that \[\begin{align*} &4(3n^2+50)-4n(2n+15) <0\\ \iff\quad & (3n^2+50)-n(2n+15) <0\\ \iff\quad & n^2 -15n +50 <0\\ \iff\quad & (n-5)(n-10) <0.\\ \end{align*}\]We can now sketch the graph of \(y = (n-5)(n-10)\).
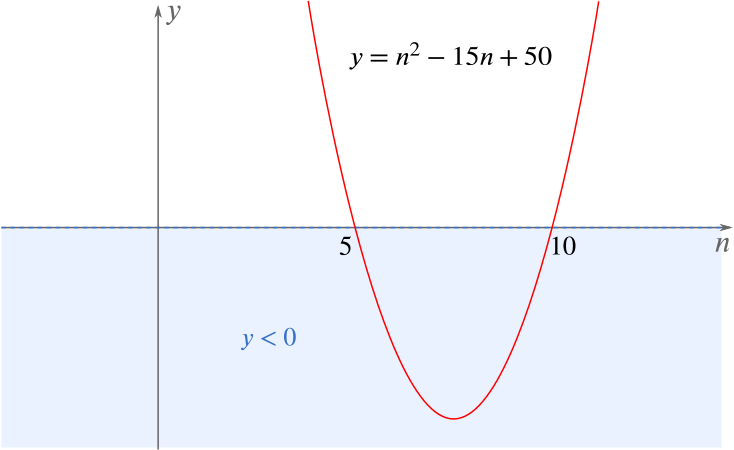
We can therefore see that \(n^2-15n+50<0\) when \(5<n<10\).
Since \(n\) is a positive integer, we deduce that the equation \(\eqref{eq:1}\) has no real roots when \(n=6\), \(7\), \(8\) or \(9\).
- Prove that if \(p < r\) and \(4q(p-r) > s^2\), then \(\eqref{eq:starrepeat}\) has no real roots for any value of \(n\).
In order for \(\eqref{eq:starrepeat}\) to have no real roots for a particular value of \(n\), its discriminant must be negative for that value of \(n\).
In order for \(\eqref{eq:starrepeat}\) to have no real roots for any value of \(n\), its discriminant must therefore be negative for all values of \(n\).
The discriminant of \(\eqref{eq:starrepeat}\) is \[4(pn^2+q)-4n(rn+s)=4(p-r)n^2-4sn+4q,\] so we want to show that \[4(p-r)n^2-4sn+4q<0\] for all values of \(n\), or equivalently, \[\begin{equation} (p-r)n^2-sn+q<0 \label{eq:2} \end{equation}\]for all \(n\). But this is a quadratic inequality in \(n\), and we want to show that it holds for all values of \(n\). (Actually, we only need to show that it is true for positive integer values of \(n\). If, though, we can show that it is true for all real values of \(n\), this will be stronger than we need and so we will be done.)
First note that \(p<r\) (which we are given) means that the leading coefficient of this quadratic is negative, so we know this quadratic is “vertex-up”:
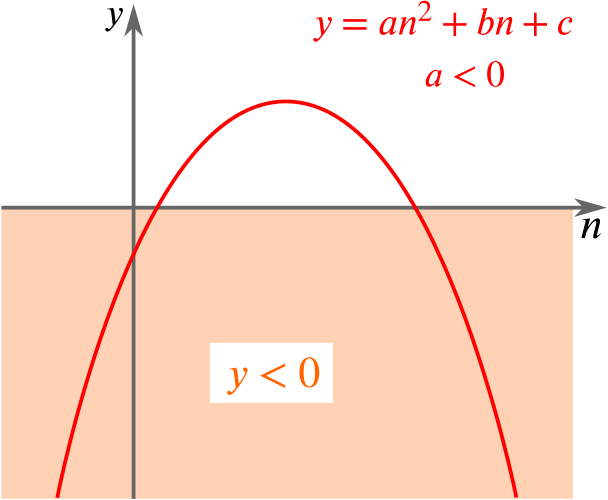
In order for this quadratic to be negative for all real \(n\), it must have no real roots.
The discriminant of the quadratic in \(\eqref{eq:2}\) is \[s^2-4(p-r)q,\] which is negative, as we are told in the question. So in this case, \(\eqref{eq:starrepeat}\) has no real roots for any value of \(n\).
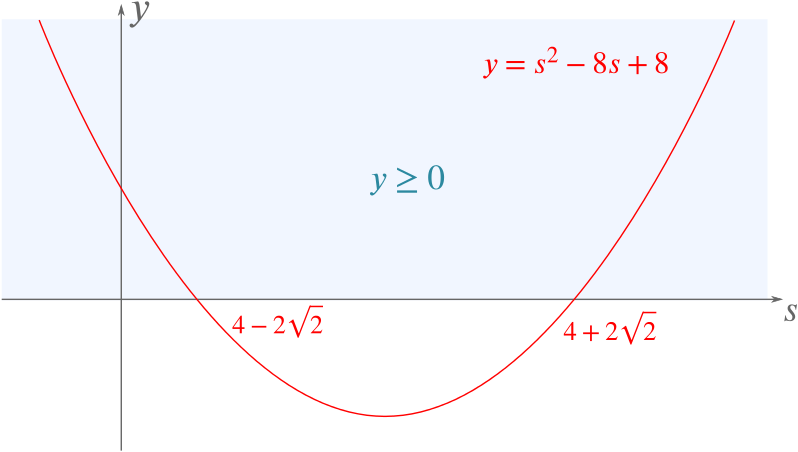
- If \(n=1\), \(p-r=1\) and \(q=s^2/8\), show that \(\eqref{eq:starrepeat}\) has real roots if, and only if, \(s\le 4-2\sqrt{2}\) or \(s\ge 4+2\sqrt{2}\).
(Alternatively, we could have used the quadratic formula for this.)
Sketching the graph of \(y=s^2-8s+8\), we see that it is non-negative if and only if \[s\ge 4+2\sqrt{2} \text{ or } s\le 4-2\sqrt{2}.\]