We will solve the equations by substitution, rearranging the first (linear) equation and substituting it into the second (quadratic) equation.
We have two choices: we could either write \(2x\) in terms of \(y\) or write \(4y\) in terms of \(x\).
Looking at the second equation, we notice that the \(x\) terms (\(4x^2=(2x)^2\) and \(20x=10(2x)\)) can be easily written in terms of \(2x\), though the coefficients involved are somewhat large, especially if we do not happen to have a calculator handy.
On the other hand, the \(y\) terms (\(16y^2=(4y)^2\) and \(4y\)) are far more straightforward, so we will use this substitution.
We can rearrange the first equation to get \(4y = 9 - 2x\). Substituting this into the second equation, we obtain \[4x^2 + (9-2x)^2 = 20x + (9-2x) - 19.\] Expanding this gives \[4x^2 + (81 - 36x + 4x^2) = 18x - 10,\] which, by bringing everything over to the left-hand side, becomes \[8x^2 - 54x + 91 = 0.\]
We could either work to discover that this factorises as \[(4x-13)(2x-7)=0\] so that \(x=\frac{13}{4}\) or \(x=\frac{7}{2}\), or we could use the quadratic formula to reach the same conclusion.
When \(x=\frac{13}{4}\), \[y = \frac{9 - 2x}{4} = \frac{9 - \tfrac{13}{2}}{4} = \frac{5}{8},\] and when \(x = \tfrac{7}{2}\), \[y = \frac{9 - 2x}{4} = \frac{9 - 7}{4} = \frac{1}{2}.\]
So the two solutions are \[\left( \frac{13}{4}, \frac{5}{8} \right) \quad\text{and}\quad \left( \frac{7}{2}, \frac{1}{2} \right).\]
Another way of thinking about these equations is as a pair of curves in the \((x,y)\)-plane. The first equation, \[2x + 4y = 9,\] is that of a straight line. The second equation, \[4x^2 + 16y^2 = 20x + 4y - 19,\] can be rearranged into \[ \left( x - \frac{5}{2} \right)^2 + 4\left( y - \frac{1}{8} \right)^2 = \frac{29}{16}, \] which is an ellipse centred at \((\frac{5}{2},\frac{1}{8})\). In the sketch below, the lines \(y = \tfrac{1}{8}\) and \(x = \tfrac{5}{2}\) are shown in grey.
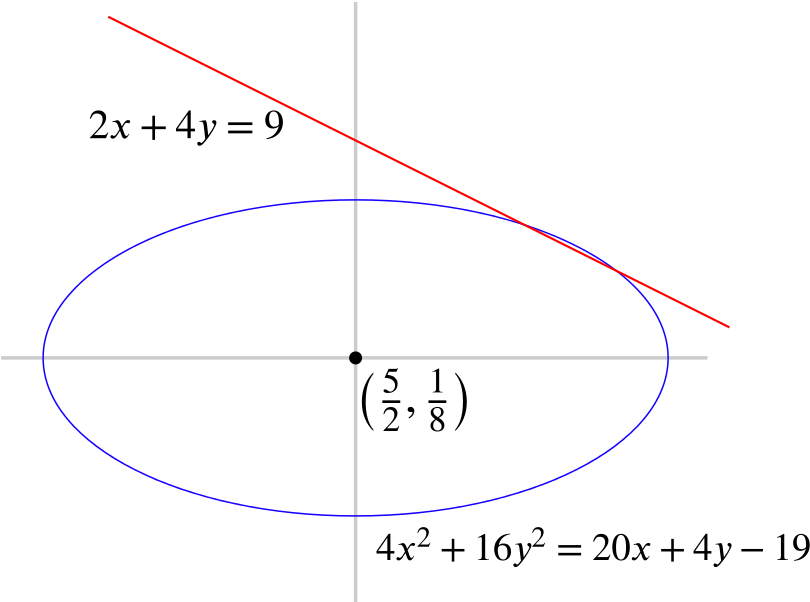
The sketch shows why there are at most two (real) solutions: a straight line and an ellipse cannot intersect more than twice.
We cannot solve this problem accurately by just sketching the graph, but it tells us something about how many solutions there could be.

