| \(x\vphantom{4}\) | \(4\) | \(7\) | \(10\) | \(13\) |
|---|---|---|---|---|
| \(\smash{y}\vphantom{4}\) | \(96\) | \(133\) | \(160\) | \(117\) |
In the above table the values of \(y\) were calculated from a formula \(y = Ax^2 + Bx\), where \(A\) and \(B\) are constants. One of the values of \(y\), however, has been deliberately misprinted.
Plot the values of \(y/x\) against those of \(x\)…We have the following calculated data:
| \(x\vphantom{4}\) | \(4\) | \(7\) | \(10\) | \(13\) |
|---|---|---|---|---|
| \(\smash{y/x}\vphantom{4}\) | \(24\) | \(19\) | \(16\) | \(9\) |
The data are plotted below.

- find which value of \(y\) has been misprinted and give the correct value,
If \(y = Ax^2 + Bx\), then \(y/x = Ax + B\).
This is the equation of a straight line, so, given the information in the question, we should expect to find a line through three of the four points plotted above. This is in fact the case!
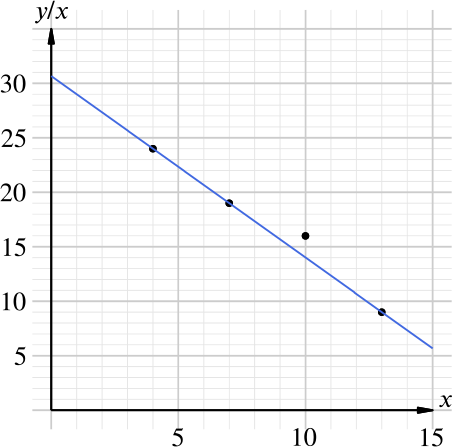
From the plot above, the incorrect value of \(y\) is the one corresponding to \(x=10\), namely \(160\).
Since the correct value of \(y/x\) must lie on the line, this value is \(14\), and so the correct value of \(y\) is \(14\times10=140\).
- estimate the numerical values of \(A\) and \(B\).
The equation of the blue line is \(y/x = Ax + B\), so we can find the value of \(A\) by finding the gradient of the line and the value of \(B\) by finding its \(y\)-intercept.
The gradient of the line in the plot above is (from looking at the points where \(x=4\) and \(x=13\)) \[ \frac{\Delta y}{\Delta x} = \frac{9 - 24}{13 - 4} = -\frac{15}{9} = -\frac{5}{3} \] so \(A = -\dfrac{5}{3}\). Taking the point with \(x=4\), \(y/x=24\), we have \[24=-\frac{5}{3}\times 4+B\] so \(B=\dfrac{92}{3}=30\frac{2}{3}\).
If we were doing this problem using real-world data rather than calculated figures, we would not use our data points to find the equation of the line (and hence \(A\) and \(B\), but would instead use points on the line itself. In this case, though, these are the same thing.

