The inequalities \(x^2 + 3x + 2 > 0\) and \(x^2 + x < 2\) are met by all \(x\) in the region:
\(x < -2\);
\(-1 < x < 1\);
\(x > -1\);
\(x > -2\).
What happens if we sketch the graphs of \(y = x^2+3x+2\) and \(y = x^2 + x -2\)?
Note that \[x^2 + 3x + 2 = (x+1)(x+2),\] so \(y= 0\) for this curve when \(x = -1\) or \(x=-2\).
Similarly, \[x^2 + x - 2 = (x-1)(x+2)\] so \(y = 0\) for this curve when \(x = 1\) or \(x=-2\).
If we draw a sketch, we can quickly see the regions where each inequality is satisfied.
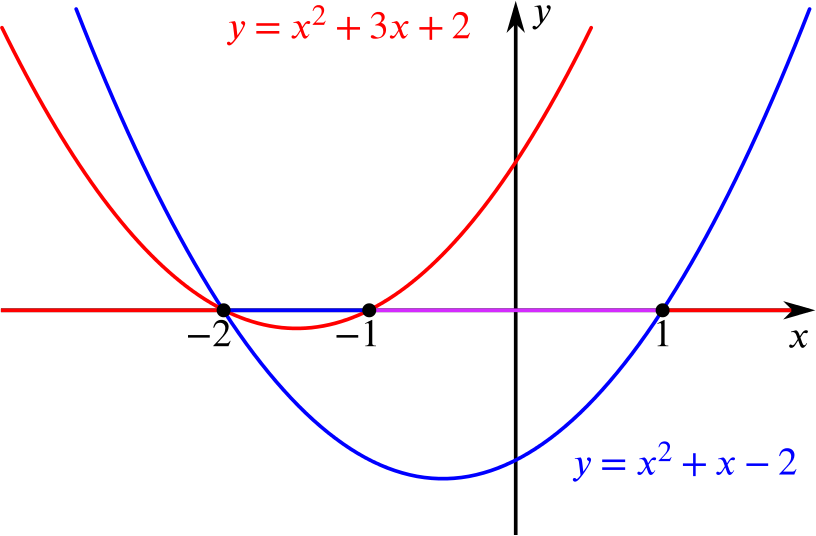
We need the region where the blue curve is below the \(x\)-axis, and where the red curve is above the \(x\)-axis.
We can see that both inequalities are satisfied in the range \(-1 < x < 1\), and the answer is (b).
For this multiple choice question, we could have been even more efficient. The second inequality \(x^2+x<2\) is only met by a finite interval of \(x\) values as the quadratic tends to infinity for large values of \(x\) (either positive or negative). The only option which offers a finite interval of \(x\) values is (b), so this must be the correct answer.

