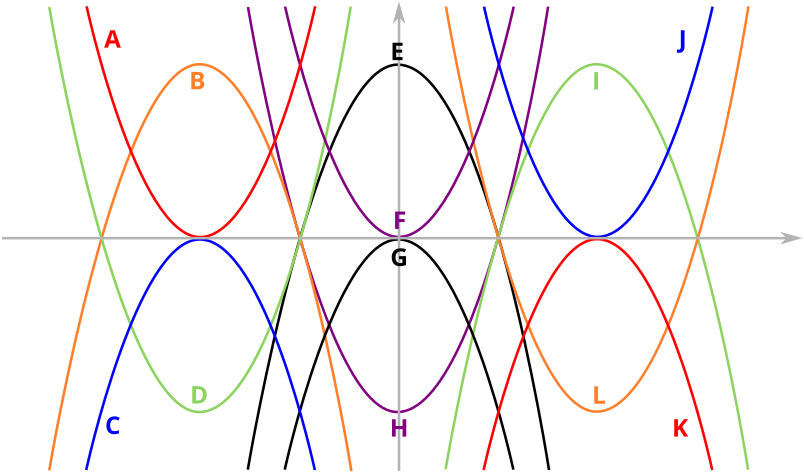
Given that two of the parabolas have the equations \[y=x^2-12x+27\] and \[y=-x^2+12x-36,\] can you find the equations of the other parabolas?
Here is a summary of the equations that you should have found.
| Parabola | Equation |
|---|---|
| A | \(y=x^2+12x+36\) |
| B | \(y=-x^2-12x-27\) |
| C | \(y=-x^2-12x-36\) |
| D | \(y=x^2+12x+27\) |
| E | \(y=-x^2+9\) |
| F | \(y=x^2\) |
| G | \(y=-x^2\) |
| H | \(y=x^2-9\) |
| I | \(y=-x^2+12x-27\) |
| J | \(y=x^2-12x+36\) |
| K | \(y=-x^2+12x-36\) |
| L | \(y=x^2-12x+27\) |
Here is a way to find the equations of the parabolas.
We will first look at the equation
\[\begin{equation} y=x^2-12x+27=(x-3)(x-9).\label{eq:1} \end{equation}\]The graph of this equation will intersect the \(x\)-axis at \(x=3\) and \(x=9\). The are only two parabolas in the picture that intersect the positive \(x\)-axis twice: parabolas I and L, which are symmetrical about the \(x\)-axis, which corresponds to the map \(y\mapsto -y\). Since the coefficient of \(x^2\) is positive, we know the parabola must look like \(\cup\) rather than \(\cap\), so the equation \(\eqref{eq:1}\) must correspond to parabola L. But we now also know what the equation of parabola I is: \(y=-x^2+12x-27\).
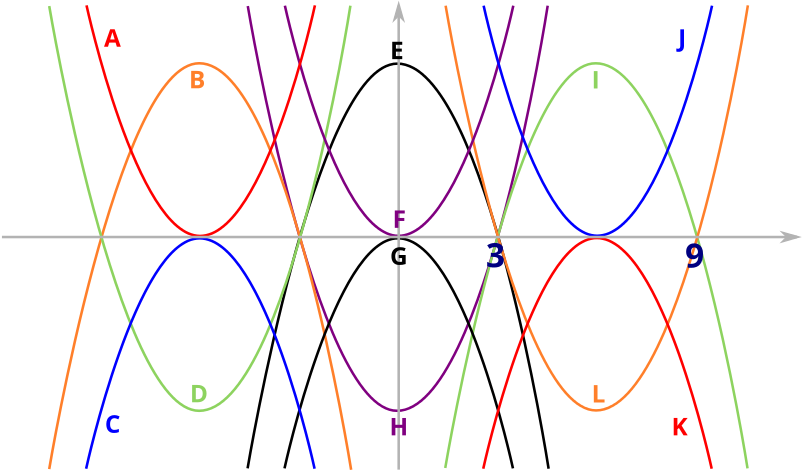
We can also see from the picture that parabola B corresponds to parabola I reflected in they \(y\)-axis. This reflection corresponds to the map \(x\mapsto -x\), so we can see that the equation of parabola B is \(y=-(-x)^2+12(-x)-27=-x^2-12x-27\). Similarly, parabola D is parabola L reflected in the \(y\)-axis, so parabola D has the equation \(y=x^2+12x+27\).
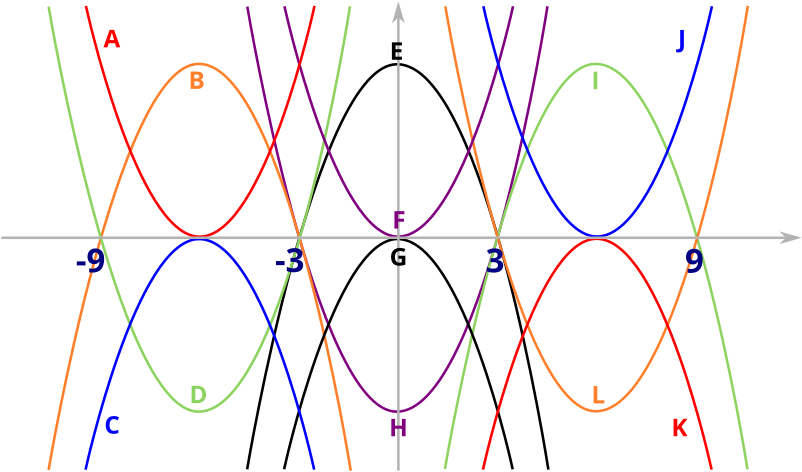
Now let’s think about the equation
\[\begin{equation} y=-x^2-12x-36=-(x+6)^2.\label{eq:2} \end{equation}\]The parabola corresponding to \(\eqref{eq:2}\) has a double root at \(x=-6\), so the top of the parabola must just touch the \(x\)-axis (the coefficient of \(x^2\) is \(-1\) so it looks like \(\cap\) rather than \(\cup\)). We know where \((-3,0)\) and \((-9,0)\) are on the picture because we know that parabola B and D intersect the \(x\)-axis at these points. Parabola A and C both have a double root at \(x=-6\), so from their shapes we see that equation \(\eqref{eq:2}\) must be the equation of parabola C, and that the equation of parabola A, its reflection in the \(x\)-axis, must have the equation \(y=(x+6)^2=x^2+12x+36\).
We can see from the picture that parabolas J and K are parabolas A and C reflected in the \(y\)-axis respectively. So parabola J must have the equation corresponding to parabola A under the transformation \(x\mapsto -x\), which is \(y=x^2-12x+36\). Similarly, parabola K has the equation \(y=-x^2+12x-36\).
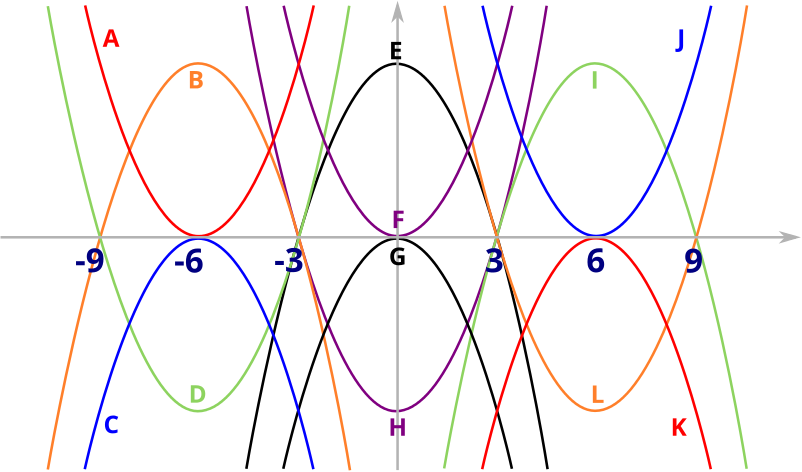
We still need to find the equations of parabolas E, F, G and H. From the picture, we see that E and H both intersect the \(x\)-axis at the points \((3,0)\) and \((-3,0)\), so they look like \(y=\pm\alpha(x+3)(x-3)\), for some \(\alpha>0\). From their shapes, we see that parabola E has equation \(y=-\alpha(x+3)(x-3)=-\alpha x^2+9\alpha\) and parabola H has equation \(y=\alpha x^2-9\alpha\). To find the value of \(\alpha\), we compare to parabola I, which has the same height. The peak of parabola I is in the middle of its two roots, since a parabola is symmetrical. So the height of parabola I, and therefore of E, is \(9\). Since the peak of parabola E is at \(x=0\), we require that \(9=0^2\alpha+9\alpha\), and so \(\alpha=1\).
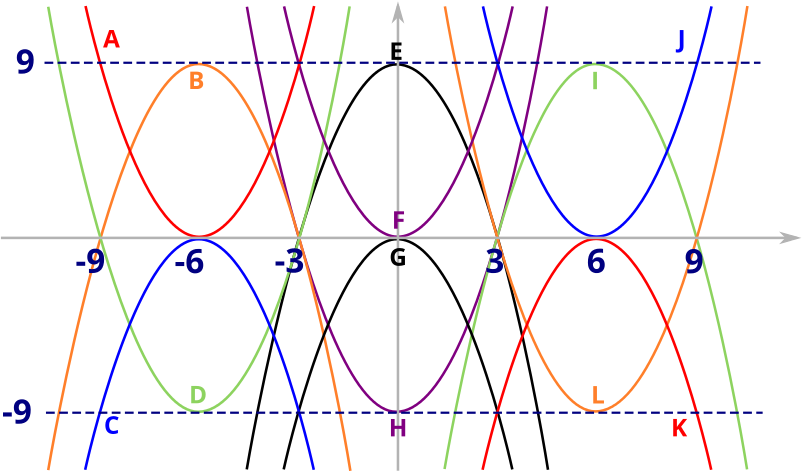
Finally, parabolas F and G both have a double root at \(x=0\), which means they have the form \(y=\pm \alpha x^2\), for some \(\alpha>0\). Again looking at their shapes, we see that parabola F has equation \(y=\alpha x^2\) and parabola G has equation \(y=-\alpha x^2\). To find the value of \(\alpha\), notice that parabola F is a translation of parabola J along the \(x\)-axis by \(6\) in the negative direction. So the equation of parabola F must be that of parabola J evaluated at \((x+6)\) instead of \(x\), and so is \(y=(x+6)^2-12(x+6)+36=x^2+12x+36-12x-72+36=x^2\). So \(\alpha=1\).

