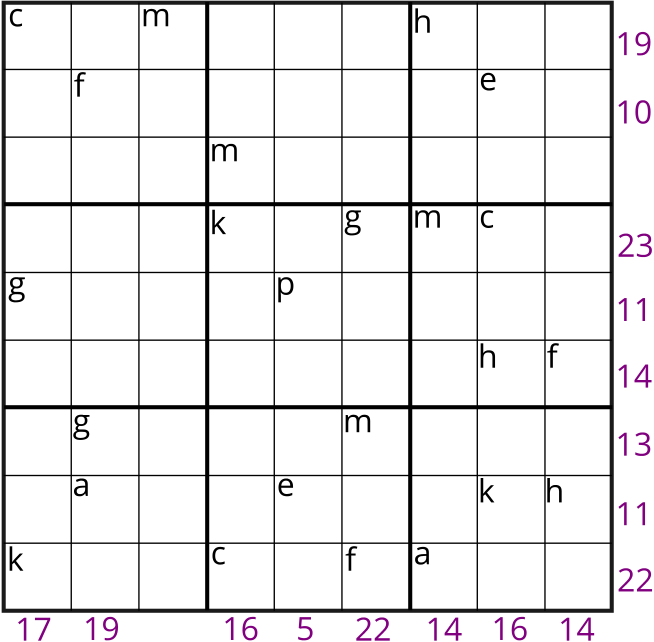
A Sudoku puzzle has two basic rules:
Each column, each row and each box (\(3\times3\) subgrid) must have the numbers \(1\) to \(9\).
No column, row or box can have two squares with the same number.
Someone has replaced each number from \(1\) to \(9\) in the Sudoku puzzle above with a letter. Given that the number at the end of a row or at the bottom of a column is the sum of the letters shown in that row or column, can you find which letter corresponds to which number, and then solve the Sudoku?
Altogether a set of 16 equations can be formed.
For example, in the first and second columns beginning from the left of the \(9\times9\) grid, we can form the following equations: \[c + g + k = 17,\] \[f + g + a = 19.\] In the fourth and fifth rows beginning from the top of the \(9\times9\) grid, the following equations can be formed: \[k + g + m + c = 23,\] \[g + p = 11.\]
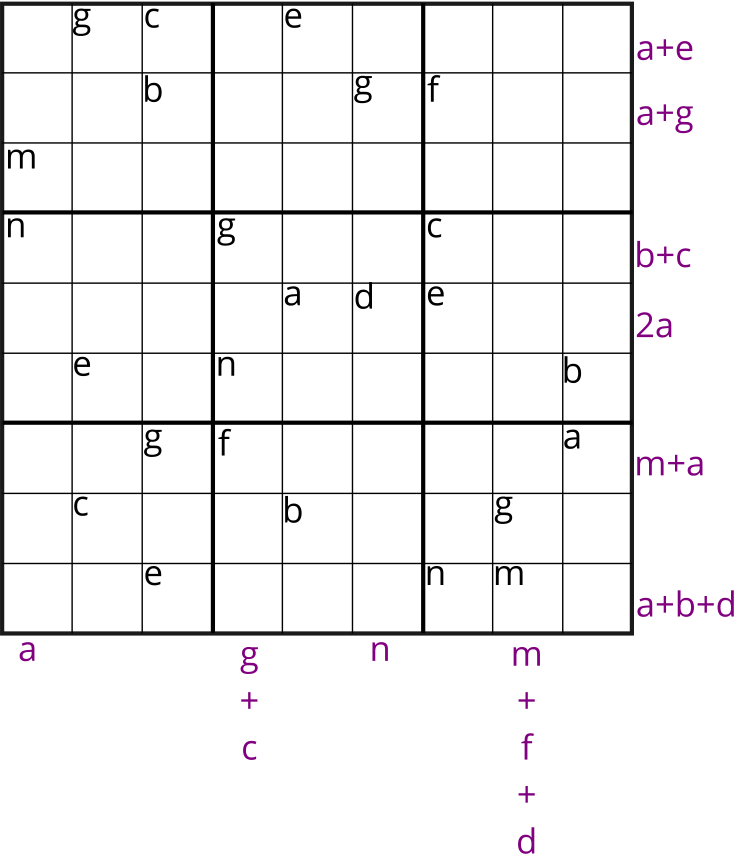
Now the numbers at the ends of the rows and columns have been replaced with letters too! Can you solve the ten equations and then solve the Sudoku?
For example, in the first and fourth columns beginning from the left of the \(9\times9\) grid, we can form the following equations: \[m + n = a,\] \[g + n + f = g + c.\] In the second and last rows beginning from the top of the \(9\times9\) grid, the following equations can be formed: \[b + g + f = a + g,\] \[e + n + m = a + b + d.\]

